Statistische Datenanalyse
Die Statistik stellt ein unentbehrliches Instrument zur Beschreibung von Daten, deren Verteilungen und Zusammenhänge sowie zur Prüfung von Hypothesen dar. Die statistische Datenanalyse beginnt mit dem Vorliegen eines aufbereiteten und fehlerbereinigten Datensatzes. In einem ersten Schritt werden Variablen umgeformt oder neu gebildet und Skalen geprüft. Ein einem zweiten Schritt wird eine deskriptive Beschreibung der Daten vorgenommen (Deskriptive Statistik), in einem dritten folgt das Testen von Hypothesen im Rahmen der schliessenden Statistik (Inferenzstatistik). Mehrheitlich erfolgt die Analyse quantitativer Daten mit einer computerunterstützten Analyse-Software wie beispielsweise SPSS.
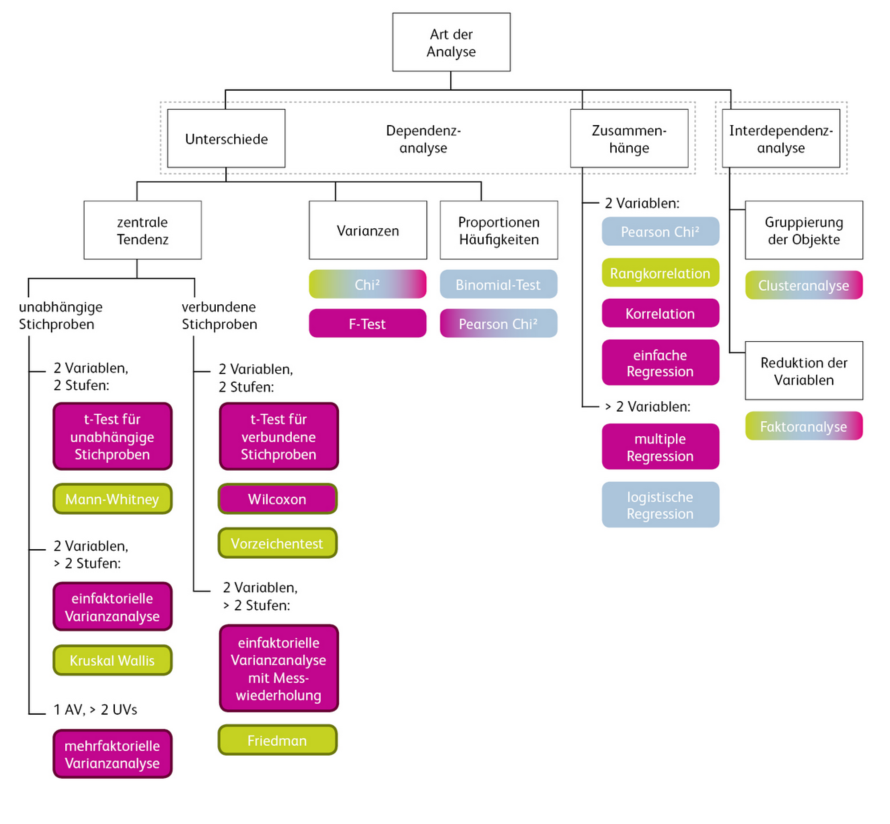
Allgemeiner Entscheidbaum

Hier geht es zum Entscheidbaum der Homepage Empirical Methods.
Recodierung, Itemanalysen, Bildung von Indizes und Codebook
Nach der abgeschlossenen Fehlerkontrolle und -bereinigung sind in der Regel Variablenumformungen (Recodierungen) sowie Neubildungen von Variablen (Indizes) des Datensatzes erforderlich. Bei der Recodierung werden beispielsweise Einkommen in Klassen zusammengefasst, da sie für die Analyse weniger differenziert erforderlich sind, als sie erfasst wurden (Befehl „Recode“ in SPSS). Bei der Neubildung von Variablen (Befehl „Compute“ in SPSS) können beispielsweise die Summen von Itemwerten einer Likert-Skala pro Person addiert und als neu gebildete Variable „Summenscore“ in den Datensatz einfliessen.Das korrekte Transformieren von Informationen in eine von Computer lesbare Form erfordert ein systematisches Vorgehen. Dies wird mit Hilfe eines so genannten Codebooks vorgenommen, in welchem das Codier-Prozedere und dessen Regeln detailliert festgelegt sind. Das Codebook stellt somit den Schlüssel zu den Daten dar und verhindert ein Sich-Verlieren in der Datenmenge und als mögliche Folge ein Neucodieren der Daten.

Datenanalyse im Hinblick auf das Forschungsproblem
Mit der deskriptiven Statistik werden mit statistischen Mitteln Beschreibungen der Stichprobe vorgenommen. Grundsätzlich wird zwischen univariaten (Analyse eines Merkmals), bivariaten (Analyse zweier Merkmale) und multivariaten (Analysen dreier und mehr Merkmale) Analysen unterschieden.
Eine wichtige Voraussetzung bei der Datenanalyse ist die Verständigung über das jeweils vorliegende Skalenniveau, da dieses die anwendbaren Auswertungsmethoden determiniert.
Deskriptive Statistik
Univariate Analysen
Bei univariaten Analysen werden Häufigkeitstabellen, Diagramme sowie Mittelwert- und Streumasse erstellt und analysiert.
Häufigkeitstabellen geben Auskunft über die Anzahl Personen und die Prozentzahl jeder Kategorie der betreffenden Variable. Intervall-/ratio-skalierte Variablen wie beispielsweise das Alter müssen dafür gruppiert (recodiert) werden. Weiter werden für univariate Analysen grafische Darstellungen eingesetzt: Balkendiagramme für nominal-/ordinal-skalierte Daten, Histogramme für intervall-/ratio-skalierte Daten. An diesen kann abgelesen werden, wie die Verteilung einer Variable charakterisiert ist (normalverteilt, rechts- resp. linksschief, etc.). Weiter werden die Mittelwerte wie Modus, Median und Mittelwert der Stichprobe definiert. Das Arithmetische Mittel (Mittelwert) erfordert ein mindestens intervall-skaliertes Skalenniveau. Der Modus ist diejenige Ausprägung einer Variablen, welche die maximale Häufigkeit aufweist. Der Median ist jener Variablenwert, bei dem die relative kumulierte Häufigkeit 0.5 erreicht und daher die Verteilung in 50% vor und 50% nach Median teilt.
Der Vergleich der Mittelwerte untereinander definiert schliesslich die Verteilung der Variable, wobei gilt:
- Modus < Median < arithm. Mittelwert => rechtsschiefe Verteilung
- Modus > Median > arithm. Mittelwert => linksschiefe Verteilung
- Modus = Median = arithm. Mittelwert => Normalverteilung (unimodal symmetrische Verteilung)
Weitere Masse zur deskriptiven Beschreibung der Stichprobe sind die Streumasse. Hierbei sind die Spannweite (Differenz zwischen maximalem und minimalem Wert der Verteilung), die Standardabweichung (Streuung der Werte einer Zufallsvariablen um ihren Mittelwert) sowie die Varianz (Quadrat der Standardabweichung) von Bedeutung.
Bivariate Analysen
Bivariate Analysen untersuchen den Zusammenhang zweier Variablen. Dabei wird ausschliesslich die Stärke des Zusammenhangs, nicht aber deren Kausalität ermittelt.
Grundsätzlich kommen, je nach Skalentyp der unabhängigen und abhängigen Variablen, Verfahren der Tabellenanalyse, Vergleich von Mittelwerten oder Korrelations- und Regressionsanalysen zum Einsatz. Die ermittelten Stärken des Zusammenhangs werden auf deren Signifikanz geprüft.
Schliessende Statistik
Während mit der deskriptiven Statistik einzig die Stichprobe beschreiben wird, werden im Rahmen der schliessenden Statistik (Inferenzstatistik) mit den Resultaten der Stichprobe bestimmte Aussagen zur Grundgesamtheit gemacht. In der schliessenden Statistik werden Signifikanztests, Verteilungs- oder Mittelwertvergleiche vorgenommen.
Mit der Analyse von Stichproben stellt sich daher die Frage, inwiefern die Resultate für die Grundgesamtheit generalisiert werden können. Zudem besteht die Gefahr eines Stichprobenfehlers (Sampling Error), eines bestehenden Unterschieds zwischen der Population und der Stichprobe, die gezogen wurde. Dies hat zur Folge, dass die Stichprobe nicht repräsentativ ist und ungültige Resultate darstellt. Im Rahmen von statistischen Signifikanztest kann gesagt werden, mit welcher Wahrscheinlichkeit (Signifikanzniveau) die Resultate einer Stichprobe auf die Grundgesamtheit übertragen werden können (ob sie oder nicht übertragen werden können, kann nicht definiert werden, nur eine Wahrscheinlichkeit). Signifikanztests zeigen die folgende Struktur:
- Aufsetzen einer negativ formuliertes Nullhypothese („es besteht in der Grundgesamtheit kein Zusammenhang zwischen zwei Variablen“ )
- Definition eines akzeptablen Signifikanzniveaus von 5% resp. 1% (α-Fehler)
- Definieren der statistischen Signifikanz der Resultate mittels Tests
- Analyse der Testresultate: Sind sie signifikant, kann die Nullhypothese verworfen werden
Grundsätzlich können beim statistischen Testen zwei Arten von Fehlern auftreten: α-Fehler (Typ-I-Error) und β-Fehler (Typ-II-Error). Bei einem α-Fehler wird die Nullhypothese verworfen, obwohl sie bestätigt werden sollte (d.h. obwohl in der Grundgesamtheit ein Zusammenhang besteht). Bei einem β-Fehler wird die Nullhypothese akzeptiert, obwohl sie verworfen werden sollte (d.h. obwohl in der Grundgesamtheit kein Zusammenhang besteht).
Zusätzlich zu Signifikanztests werden in der schliessenden Statistik weiter Verteilungsvergleiche (Chi-Quadrat-Tests) oder Mittelwertvergleiche (T-Tests) vorgenommen.
Multivariate Analysen
Bei experimentellen Designs können Einflüsse von Drittvariablen durch den Einsatz von Kontroll- und Experimentalgruppen kontrolliert werden. Anders verhält es sich bei nicht-experimentellen Designs, wo bei bivariaten Analysen die Gefahr besteht, dass Zusammenhänge auf Einflüssen von Drittvariablen basieren. Daher wird in multivariaten Analysen versucht, Drittvariablen durch statistische Techniken unter Kontrolle zu bringen. Hierzu ist erforderlich, dass eine Hypothese über den potenziellen Effekt einer Drittvariable vorliegt sowie dass Messdaten zur Drittvariable vorliegen.
Grundsätzlich werden multivariate Analysen in folgenden drei Kontexten eingesetzt um zu beweisen:
- dass ein Zusammenhang zwischen Variablen nicht zufällig ist (reeller Zusammenhang),
- dass ein indirekter Zusammenhang zweier Variablen durch eine dritte beeinflusst ist, sowie
- dass eine dritte Variable die Beziehung zwischen zwei Variablen moderiert.
Für die multivariate Analyse stehen verschiedene Verfahren wie Faktorenanalysen, Clusteranalysen oder Regressionsanalysen zur Verfügung.
Allenfalls erweist sich nach der Prüfung von Zusammenhängen ein Zurückkehren zur Datenaufbereitung und das Bilden neuer zu prüfender Variablen als sinnvoll.