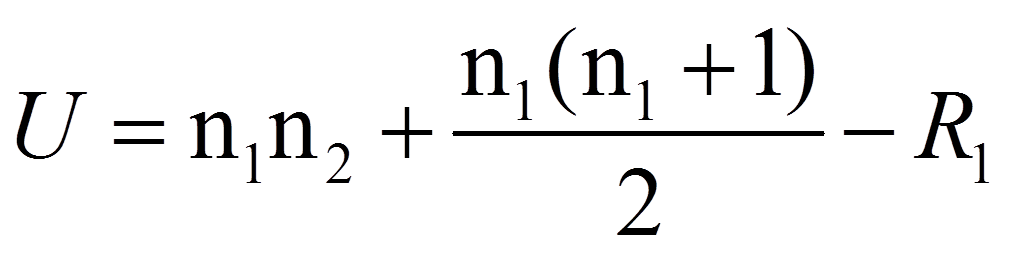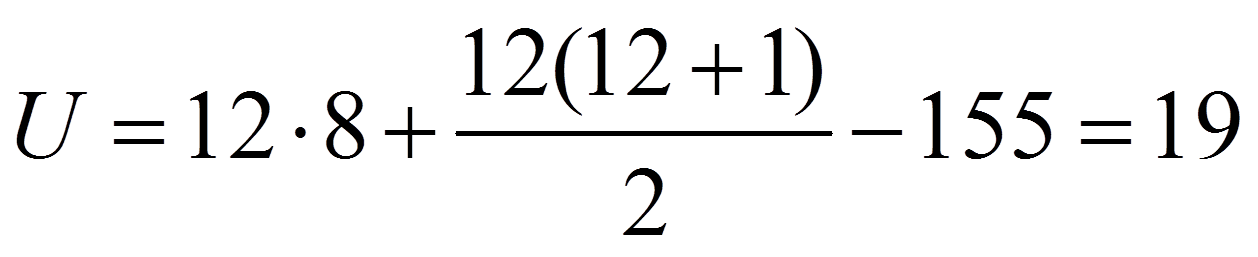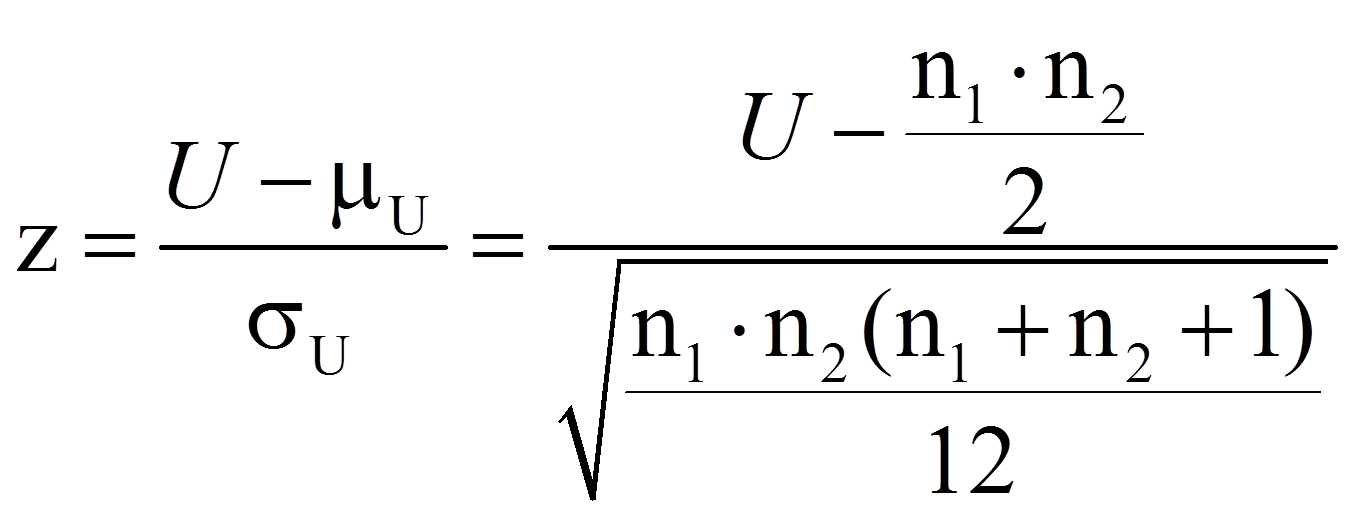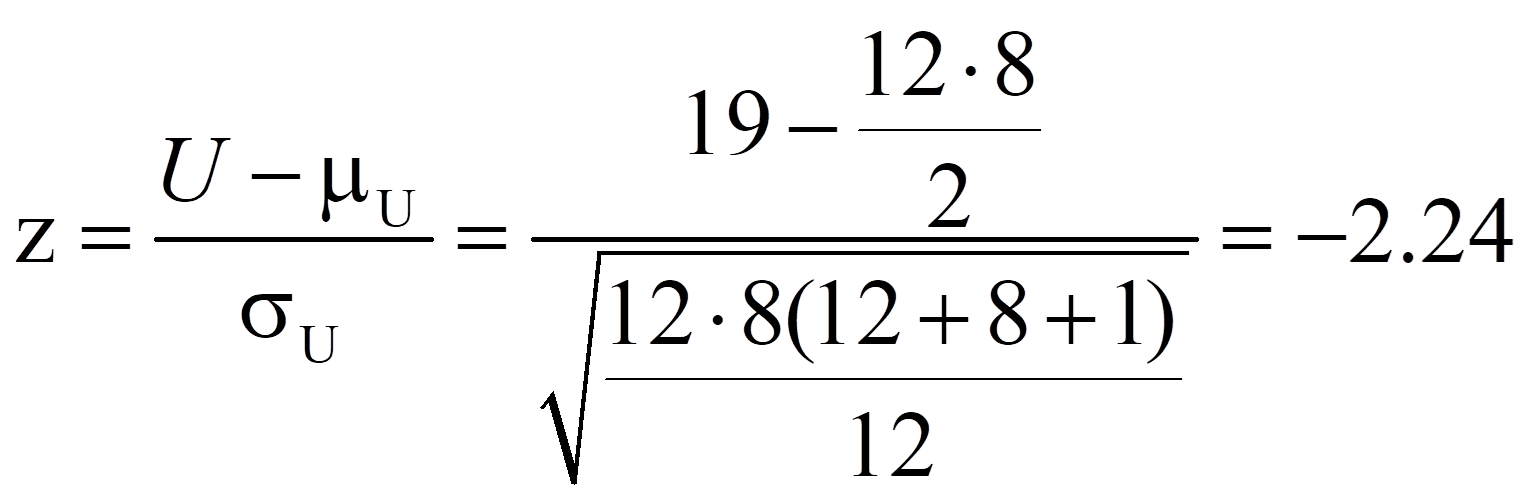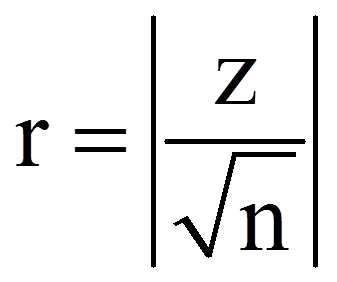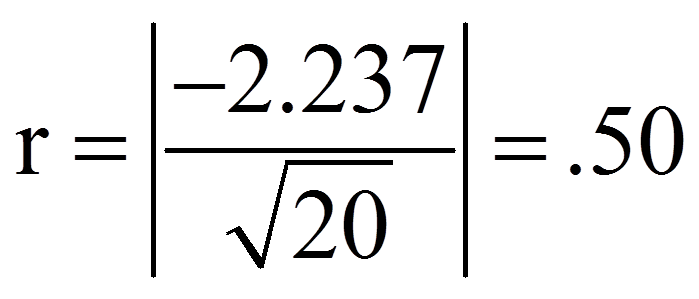 Quick Start
Quick Start1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen des Mann-Whitney-U-Tests
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Berechnung der Teststatistik
3. Mann-Whitney-U-Test mit SPSS
3.1. SPSS-Befehle
3.2. Ergebnisse des Mann-Whitney-U-Tests
3.3. Berechnung der Gruppenmediane für die Berichterstattung
3.4. Berechnung der Effektstärke
3.5. Eine typische Aussage
Quick Start
| Wozu wird der Mann-Whitney-U-Test verwendet? Der Mann-Whitney-U-Test für unabhängige Stichproben testet, ob die zentralen Tendenzen zweier unabhängiger Stichproben verschieden sind. Der Mann-Whitney-U-Test wird verwendet, wenn die Voraussetzungen für einen t-Test für unabhängige Stichproben nicht erfüllt sind. SPSS-Menü
Analysieren > Nichtparametrische Tests > Klassische Dialogfelder > Zwei unabhängige Stichproben SPSS-Syntax
NPAR TESTS /M-W=abhängige Variable BY Gruppen (1 2) /STATISTICS=DESCRIPTIVES SPSS-Beispieldatensatz
Mann-Whitney-U-Test |
1. Einführung
Der Mann-Whitney-U-Test – auch „Wilcoxon Rangsummen-Test“ genannt (engl. „Wilcoxon rank-sum test“, kurz: WRS) – für unabhängige Stichproben testet, ob die zentralen Tendenzen zweier unabhängiger Stichproben verschieden sind. Der Mann-Whitney-U-Test wird verwendet, wenn die Voraussetzungen für einen t-Test für unabhängige Stichproben nicht erfüllt sind.
Der Mann-Whitney-U-Test ist das nichtparametrische Äquivalent des t-Tests für unabhängige Stichproben und wird angewandt, wenn die Voraussetzungen für ein parametrisches Verfahren nicht erfüllt sind. Nicht-parametrische Verfahren sind auch bekannt als „voraussetzungsfreie Verfahren“, weil sie geringere Anforderungen an die Verteilung der Messwerte in der Grundgesamtheit stellen. So müssen die Daten nicht normalverteilt sein und die Variablen müssen lediglich ordinalskaliert sein. Auch bei kleinen Stichproben und Ausreissern kann ein Mann-Whitney-U-Test berechnet werden.
Die Fragestellung des Mann-Whitney-U-Tests für unabhängige Stichproben wird oft so verkürzt:
„Unterscheiden sich die zentralen Tendenzen zweier unabhängiger Stichproben?“
1.1. Beispiele für mögliche Fragestellungen
- Unterscheiden sich die Schulnoten von Mädchen und Jungen?
- Zeigen sich Unterschiede zwischen Rechts- und Linkshändern auf einer Depressionsskala?
- Zeigen Kinder, die unter der Woche nicht Fernsehen dürfen, höhere Werte in einem Aufmerksamkeitstest, als solche, die Fernsehen dürfen?
- Zeigen sich Unterschiede in der Darlehenshöhe zwischen Kreditnehmern, die den Kredit zurückgezahlt haben, und solchen, die dies versäumt haben?
1.2. Voraussetzungen des Mann-Whitney-U-Tests
| ✓ | Die abhängige Variable ist mindestens ordinalskaliert |
| ✓ | Es liegt eine unabhängige Variable vor, mittels der die beiden zu vergleichenden Gruppen gebildet werden |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
20 Patienten einer Klinik werden untersucht. 12 davon sind in kardiologischer Behandlung, während 8 dies nicht sind. Sie alle beantworten einen Fragebogen zum allgemeinen Wohlbefinden (Werte von 0 bis 35, 0 steht für ein sehr hohes, 35 für ein sehr geringes Wohlbefinden). Es soll geprüft werden, ob es Unterschiede hinsichtlich der zentralen Tendenz des Wohlbefindens zwischen den Herzpatienten und den übrigen Patienten gibt.
Der zu analysierende Datensatz enthält neben der Probandennummer (ID), die Gruppierungsvariable (Group), welche für Herzpatienten den Wert 1 annimmt und für andere Patienten den Wert 2, und dem Wert für das Wohlbefinden (Data).
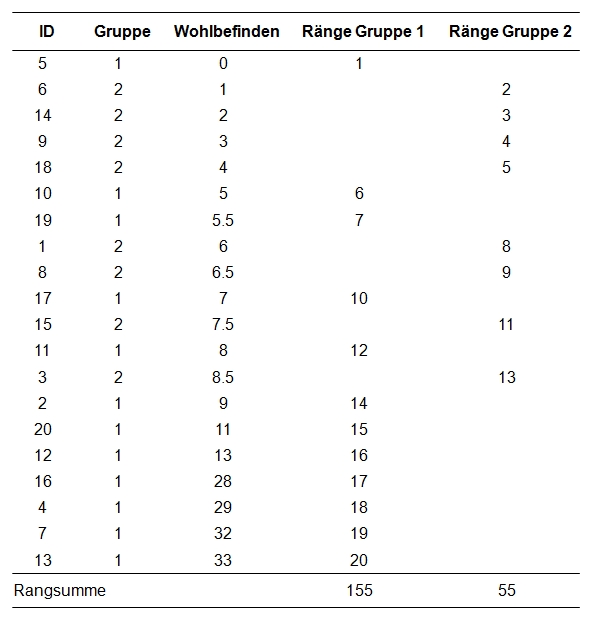
Abbildung 1: Beispieldaten und erste Berechnungsschritte (Gruppe 1 = Herzpatient, Gruppe 2 = kein Herzpatient)
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Berechnung der Teststatistik
Der Mann-Whitney-U-Test basiert auf der Idee der Rangierung der Daten. Das heisst, es wird nicht mit den Messwerten selbst gerechnet, sondern diese werden durch Ränge ersetzt, mit welchen der eigentliche Test durchgeführt wird. Damit beruht die Berechnung des Tests ausschliesslich auf der Ordnung der Daten (grösser als, kleiner als). Die absoluten Abstände zwischen den Werten werden nicht berücksichtigt.
Zuerst werden die einzelnen Messwerte gemäss ihrer Grösse (von den kleinsten Werten aufsteigend) aufgereiht (siehe Abbildung 1, Spalte „Wohlbefinden“). Dies geschieht unabhängig von der Gruppenzugehörigkeit (Spalte „Gruppe“). Danach werden die Messwerte rangiert (von 1 ausgehend und aufsteigend) und getrennt für jede Gruppe notiert. Diese Ränge sind in Abbildung 1 in den Spalten „Ränge Gruppe 1“ und „Ränge Gruppe 2“ enthalten. Kommt ein Messwert mehrfach vor (engl. „ties“), so werden sogenannte „verbundene Ränge“ gebildet. Wenn beispielsweise Rang 5 und 6 beide die gleichen Messwerte aufweisen, wird aus diesen beiden der Mittelwert gebildet ((5 + 6)/2 = 5.5) und die Ränge 5 und 6 werden neu beide mit dem Rang 5.5 versehen.
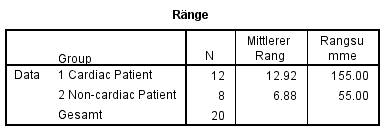
Schliesslich werden für beide Gruppen Rangsummen gebildet (siehe Abbildung 1, Zeile „Rangsummen“). Hierfür werden lediglich die Ränge der jeweiligen Gruppe aufsummiert. Dies ergibt eine Rangsumme von 155 für die Herzpatienten (n = 12) und 55 für die übrigen Patienten (n = 8). Zur Berechnung der Teststatistik U wird anschliessend die grössere der beiden Rangsummen verwendet:
Signifikanz der Teststatistik
Bei hinreichend grosser Stichprobe (n1 + n2 > 30) kann die Signifikanz geprüft werden, indem der eben berechnete U-Wert wie folgt z-standardisiert wird:
Dieser z-Wert kann nun auf Signifikanz geprüft werden, indem er mit dem kritischen Wert der Standardnormalverteilung (z-Verteilung) verglichen wird. Dieser kritische Wert kann Tabellen entnommen werden. Für das zweiseitige Signifikanzniveau .05 beträgt er ±1.96. Ist der Betrag der Teststatistik höher als der kritische Wert, so ist der Unterschied signifikant. Dies ist für das Beispiel der Fall (|-2.24| > 1.96). Es kann also davon ausgegangen werden, dass sich die beiden zentralen Tendenzen unterscheiden (exakter Mann-Whitney-U-Test: U = 19, p < .05).
3. Mann-Whitney-U-Test mit SPSS
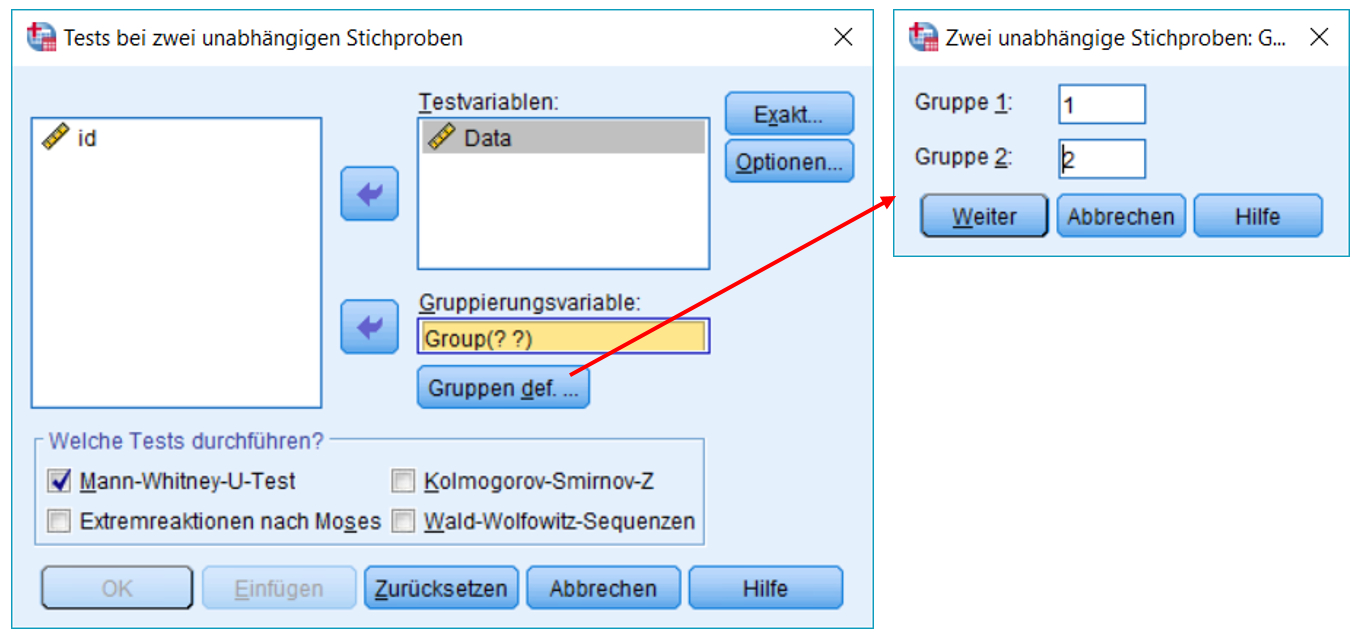
3.1. SPSS-Befehle
SPSS-Menü: Analysieren > Nichtparametrische Tests > Klassische Dialogfelder > Zwei unabhängige Stichproben
Hinweis
- Da die unabhängige Variable (Gruppenvariable) mehr als zwei Gruppen unterscheiden könnte, müssen unter Gruppen def. … jene Werte angegeben werden, welche die beiden Gruppen beschreiben. Hier sind das 1 und 2, da im Datensatz die Herzpatienten als 1 und übrigen Patienten als 2 codiert wurden.
SPSS-Syntax
NPAR TESTS
/M-W= Data BY Group(1 2)
/STATISTICS=DESCRIPTIVES
/MISSING ANALYSIS.
3.2. Ergebnisse des Mann-Whitney-U-Tests
Die deskriptiven Statistiken, die SPSS für den Mann-Whitney-U-Test ausgibt, sind wenig nützlich, da die Werte nicht getrennt nach Gruppenzugehörigkeit ausgegeben werden (siehe Abbildung 3).
Die Tabelle „Ränge“ (Abbildung 4) zeigt die beiden Gruppengrössen, die beiden Rangsummen, sowie den gemittelten Rang der beiden Gruppen (Rangsumme dividiert durch die Gruppengrösse). Ein Vergleich der beiden mittleren Ränge zeigt, dass die beiden Gruppen eine unterschiedliche zentrale Tendenz aufweisen könnten. Wären sie in etwa gleich rangiert, so wiesen sie einen ähnlichen mittleren Rang auf.
SPSS gibt in Abbildung 5 sowohl die asymptotische Signifikanz aus, als auch eine exakte Signifikanz. In Abhängigkeit von der Stichprobengrösse wird der eine oder andere Wert berichtet:
- Ist die Stichprobe hinreichend gross (n1 + n2 > 30), so wird die asymptotische Signifikanz berichtet: z = -2.237, p = .025
- Ist dies nicht der Fall, so wird die exakte Signifikanz berichtet: U = 19.000, p = .025
Da im vorliegenden Beispiel die Stichprobengrösse (n1 + n2 = 20) kleiner als 30 ist, wird auf der Basis der exakten Signifikanz gefolgert, dass sich die beiden zentralen Tendenzen unterscheiden (Mann-Whitney-U-Test: U = 19.000, p = .025).
3.3. Berechnung der Gruppenmediane für die Berichterstattung
Über das SPSS-Menü Daten > Datei aufteilen (Ausgabe nach Gruppen aufteilen: Group) lässt sich festlegen, dass SPSS alle folgenden Analysen getrennt für die Werte von Group durchführt. Anschliessend werden über das Menü Analysieren > Deskriptive Statistiken > Häufigkeiten (Statistiken: Median) die Mediane ausgegeben.
SPSS-Syntax
SORT CASES BY Group.
SPLIT FILE SEPARATE BY Group.
FREQUENCIES VARIABLES=Data
/FORMAT=NOTABLE
/STATISTICS=MEDIAN
/ORDER=ANALYSIS.
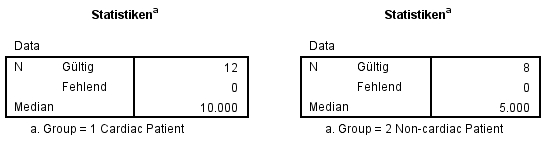
Dies führt zum folgenden SPSS-Output (Abbildung 6), der die beiden Mediane angibt:
3.4. Berechnung der Effektstärke
Um die Bedeutsamkeit eines Ergebnisses zu beurteilen, werden Effektstärken berechnet. Im Beispiel ist der Mittelwertsunterschied zwar signifikant, doch es stellt sich die Frage, ob der Unterschied gross genug ist, um ihn als bedeutend einzustufen.
Es gibt verschiedene Arten die Effektstärke zu messen. Zu den bekanntesten zählen die Effektstärke von Cohen (d) und der Korrelationskoeffizient (r) von Pearson. Der Korrelationskoeffizient eignet sich sehr gut, da die Effektstärke dabei immer zwischen 0 (kein Effekt) und 1 (maximaler Effekt) liegt. Wenn sich jedoch die Gruppen hinsichtlich ihrer Grösse stark unterscheiden, wird empfohlen, d von Cohen zu wählen, da r durch die Grössenunterschiede verzerrt werden kann.
Zur Berechnung des Korrelationskoeffizienten (r) werden der z-Wert und die Stichprobengrösse (n) verwendet, die dem SPSS-Output (Abbildungen 4 und 5) entnommen werden können. Auch wenn das Resultat des Tests auf der Basis der exakten Signifikanz beruht, kann der z-Wert für die Berechnung des Korrelationskoeffizienten verwendet werden, da SPSS diesen Wert in jedem Fall berechnet.
3.5. Eine typische Aussage
Herzpatienten weisen ein geringeres Wohlbefinden auf (Mdn = 10, tiefe Werte stehen für eine hohe Zufriedenheit) als andere Patienten (Mdn = 5), exakter Mann-Whitney-U-Test: U = 19.000, p = .025. Die Effektstärke nach Cohen (1992) liegt bei r = .50 und entspricht einem starken Effekt.