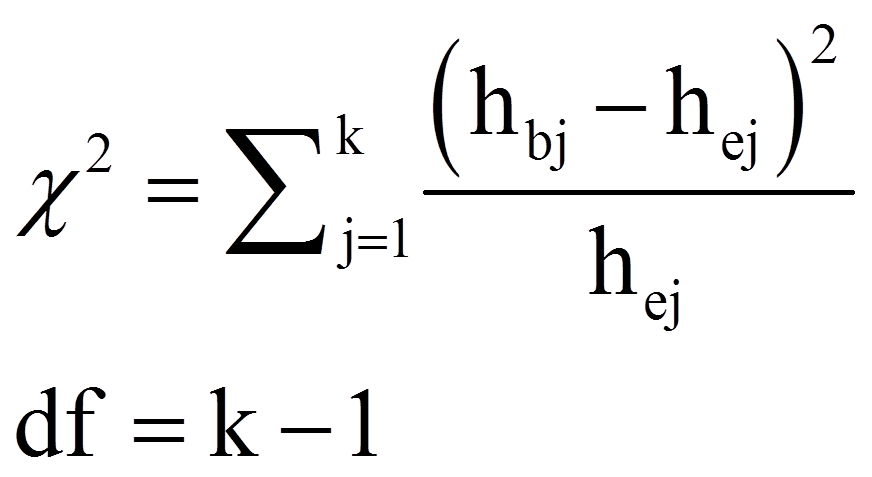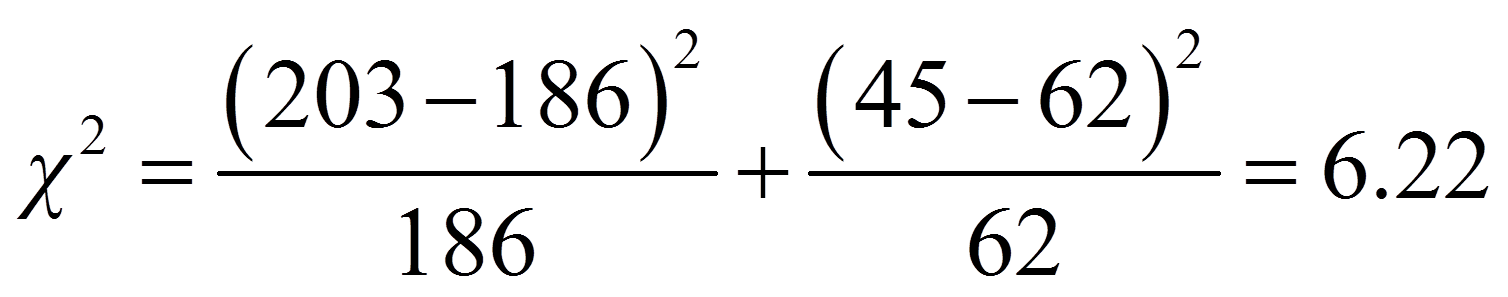 Quick Start
Quick Start
1. Einführung
2. Chi-Quadrat-Anpassungstest
2.1. Beispiele für mögliche Fragestellungen
2.2. Voraussetzungen
2.3. Beispiel einer Studie
2.4. Berechnung der Teststatistik
2.5. SPSS-Befehle
2.6. Ergebnisse
2.7. Eine typische Aussage
3. Chi-Quadrat-Test auf Normalverteilung
3.1. Beispiele für mögliche Fragestellungen
3.2. Voraussetzungen
3.3. Beispiel einer möglichen Studie
3.4. Berechnung der Teststatistik
3.5. SPSS-Befehle
3.6. Ergebnisse
3.7. Eine typische Aussage
4. Kolmogorov-Smirnov-Test auf Normalverteilung
4.1. Beispiele für mögliche Fragestellungen
4.2. Voraussetzungen
4.3. Berechnung der Teststatistik
4.4. SPSS-Befehle
4.5. Ergebnisse
4.6. Eine typische Aussage
Quick Start
| Wozu wird dieser Pearson Chi-Quadrat-Test verwendet? Um zu prüfen, ob sich die Häufigkeitsverteilung einer kategorialen Variable von einer theoretisch angenommenen Verteilung unterscheidet. SPSS-Menü
Analysieren > Nichtparametrische Tests > Klassische Dialogfelder > Chi-Quadrat SPSS-Syntax
NPAR TESTS /CHISQUARE=Variable /EXPECTED=Wert1 Wert2 Wert3 … /STATISTICS DESCRIPTIVES /MISSING ANALYSIS. NPAR TESTS /K-S(NORMAL)=Variable /STATISTICS DESCRIPTIVES /MISSING ANALYSIS. |
1. Einführung
Der Pearson Chi-Quadrat-Test wird angewandt, um zu prüfen, ob sich eine empirisch beobachtete Verteilung einer kategorialen Variable von einer bestimmten theoretisch erwarteten Verteilung unterscheidet. Die erwartete Verteilung kann dabei beliebig sein. Eine häufige Anwendung besteht darin, eine beobachtete Verteilung auf Normalverteilung zu prüfen. Hierfür wird die beobachtete Verteilung mit einer theoretischen Normalverteilung verglichen.
Dieser Test wird auch als „Chi-Quadrat-Anpassungstest“ (engl. „Goodness of fit test“), „Chi-Quadrat-Homogenitätstest“ oder „Einstichproben-Chi-Quadrat-Test“ bezeichnet.
Die Fragestellung dieses Chi-Quadrat-Tests wird oft so verkürzt: „Unterscheidet sich die beobachtete Häufigkeitsverteilung von einer erwarteten Häufigkeitsverteilung?“ oder spezifischer „Unterscheidet sich die beobachtete Verteilung einer Variable von einer Normalverteilung?“
Es wird zunächst auf den allgemeineren Fall eingegangen, wo der Vergleich mit einer beliebigen Verteilung erfolgt (Chi-Quadrat-Anpassungstest). Anschliessend wird der Spezialfall des Chi-Quadrat-Tests auf Normalverteilung vorgestellt. Am Ende des Kapitels wird kurz auf den Kolmogorov-Smirnov-Test eingegangen, welcher ebenfalls ein Test auf Normalverteilung darstellt.
2.1. Beispiele für mögliche Fragestellungen
- Besuchen mehr Mädchen oder Jungen ein Gymnasium in Luzern?
- Entspricht die Verteilung der Hotelkategorien in Leukerbad der gesamtschweizerischen Verteilung gemäss Tourismusstatistik?
- Entspricht die Verteilung der Wohnformen in einer Genossenschaft der (bekannten) Verteilung der Wohnformen auf dem freien Markt?
2.2. Voraussetzungen
| ✓ | Die Variable ist kategorial (nominal- oder ordinalskaliert) |
| ✓ | Die erwartete Häufigkeit in jeder Kategorie muss mindestens 1 betragen. Bei höchstens 20% der Kategorien darf die erwartete Häufigkeit unter 5 liegen, damit die Teststatistik näherungsweise einer Chi-Quadrat-Verteilung folgt |
2.3. Beispiel einer Studie
Eine Untersuchung hat gezeigt, dass Frauen häufiger Mobbing zum Opfer fallen als Männer. Es wird angenommen, dass das Verhältnis 3:1 ist, was bedeutet, dass Frauen dreimal so oft Mobbing in ihrer Berufslaufbahn erleben. Es soll nun getestet werden, ob dies auch in einer Stichprobe von 248 Mobbingopfern zutrifft.
Der zu analysierende Datensatz beinhaltet daher neben einer ID-Nummer für jeden Befragten (ID) das Geschlecht der Mobbingopfer (Geschlecht). Der Datensatz kann unter Quick Start heruntergeladen werden.
Beobachtete und erwartete Häufigkeiten
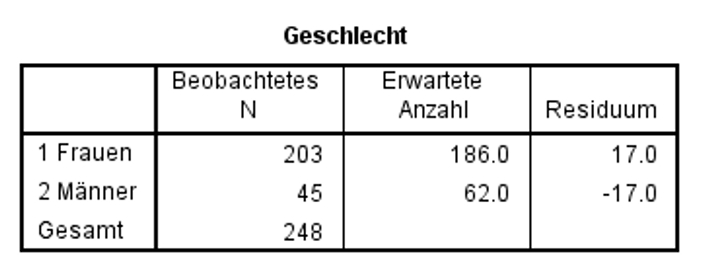
Zur manuellen Berechnung der Teststatistik werden die beobachteten (empirischen) und die erwarteten (postulierten) Häufigkeiten benötigt. Wie Abbildung 1 zeigt, sind unter den 248 Mobbingopfern 203 Frauen und 45 Männer.
Die Verteilung der erwarteten Häufigkeiten muss postuliert werden. Gemäss der Einleitung zum Beispiel wird für Mobbing ein Verhältnis von Frauen zu Männern von 3:1 erwartet. Bei 248 Personen sollten also 3/4 Frauen und 1/4 Männer sein: Dies wären 186 Frauen und 62 Männer (siehe Abbildung 1).
Berechnen der Teststatistik
Ein Vergleich der beobachteten Häufigkeiten mit den theoretisch erwarteten Häufigkeiten zeigt, dass gewisse Unterschiede vorliegen. Anhand der Teststatistik Chi-Quadrat lässt sich prüfen, wie gut die beiden Häufigkeitsverteilungen übereinstimmen:
mit
| = | Anzahl zu vergleichende Kategorien (hier k = 2: Frauen und Männer) | |
| = | beobachtete absolute Häufigkeit der Kategorie j | |
| = | erwartete absolute Häufigkeit der Kategorie j |
Das Quadrieren der Differenzen zwischen den beobachteten und erwarteten Häufigkeiten bewirkt, dass sich positive und negative Differenzen nicht gegenseitig aufheben und dass grössere Differenzen ein grösseres Gewicht erhalten.
Sind alle erwarteten Zellbesetzungen genügend gross – siehe Voraussetzungen –, so folgt die Teststatistik näherungsweise einer Chi-Quadrat-Verteilung mit Freiheitsgraden df = k-1.
Für die Beispieldaten ergibt dies:
Signifikanz der Teststatistik
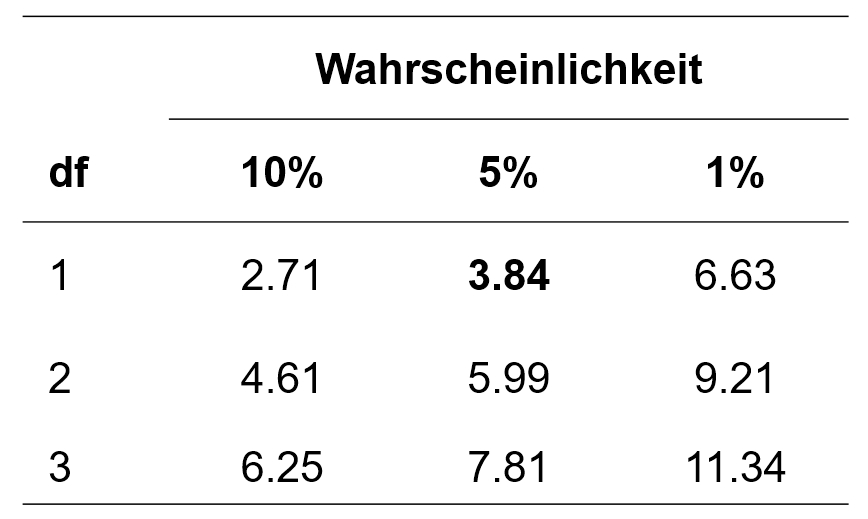
Um zu prüfen, ob die Abweichung zwischen beobachteten und erwarteten Häufigkeiten signifikant ist, wird die Teststatistik nun mit einem kritischen Wert verglichen. Dieser kritische Wert kann Tabellen entnommen werden. Abbildung 2 zeigt einen Auszug.
Für das vorliegende Beispiel beträgt der kritische Wert 3.84 bei df = 1 und α = .05 (siehe Abbildung 2). Ist der Wert der Teststatistik höher als der kritische Wert, so ist der Unterschied signifikant. Dies ist für das Beispiel der Fall (6.22 > 3.84). Daher kann davon ausgegangen werden, dass sich die beiden Verteilungen signifikant unterscheiden (Chi-Quadrat(1, n = 248) = 6.22, p = .013).
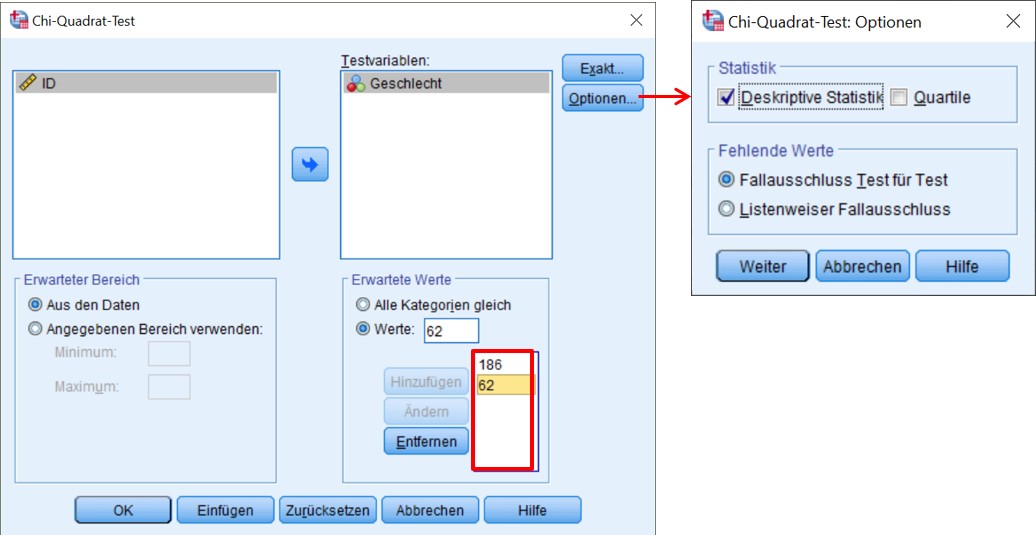
2.5. SPSS-Befehle
Hinweis
- Bei Erwartete Werte werden die erwarteten Häufigkeiten eingetragen.
SPSS-Syntax
NPAR TESTS
/CHISQUARE=Geschlecht
/EXPECTED=186 62
/STATISTICS DESCRIPTIVES
/MISSING ANALYSIS.
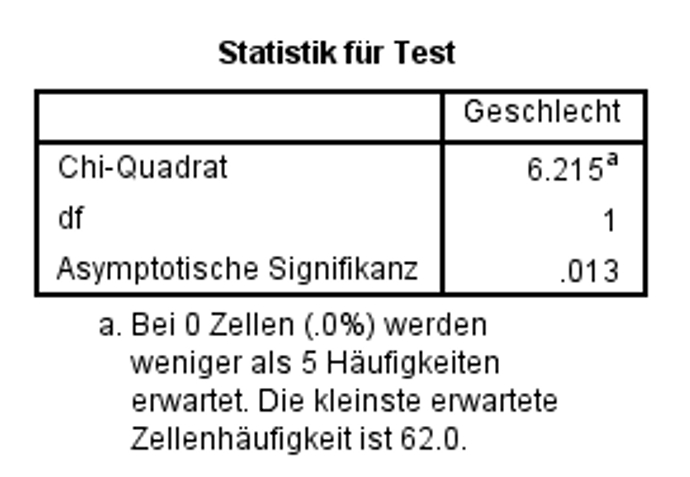
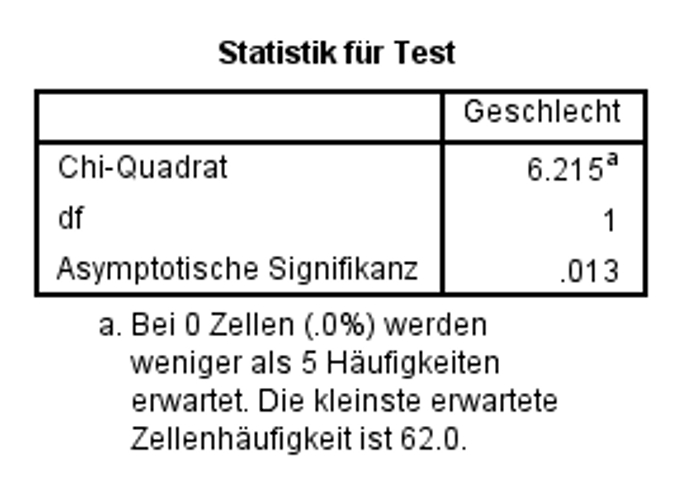
Abbildung 5 lässt sich der Wert für Chi-Quadrat entnehmen, sowie die dazugehörige asymptotische Signifikanz. Es zeigt sich, dass sich die beobachteten Häufigkeiten und die theoretisch erwarteten Häufigkeiten signifikant voneinander unterscheiden (Chi-Quadrat(1, n = 248) = 6.215, p = .013).
Damit muss die Nullhypothese verworfen werden, dass Frauen dreimal so häufig wie Männer von Mobbing betroffen sind. (Dies heisst jedoch nicht, dass keine Unterschiede zwischen den Geschlechtern bestehen. Das Ergebnis besagt lediglich, dass Verteilung signifikant von der angenommenen 3:1-Verteilung abweicht.)
2.7. Eine typische Aussage
Ein Chi-Quadrat-Anpassungstest zeigt, dass die beobachteten Häufigkeiten signifikant von den erwarteten Häufigkeiten abweichen (Chi-Quadrat(1, n = 248) = 6.215, p = .013). Damit wird die Vermutung verworfen, dass Frauen dreimal so häufig Opfer von Mobbing werden wie Männer.
3.1. Beispiele für mögliche Fragestellungen
- Ist der Intelligenzquotient in einer Schulklasse normalverteilt?
- Ist die Risikobereitschaft von jungen Männern normalverteilt?
- Folgen die Mathematiknoten einer Lehrabschlussprüfung einer Normalverteilung?
3.2. Voraussetzungen
| ✓ | Die Variable ist kategorial (nominal- oder ordinalskaliert) |
| ✓ | Alle erwarteten Zellhäufigkeiten sind ≥ 5, damit die Teststatistik näherungsweise einer Chi-Quadrat-Verteilung folgt |
3.3. Beispiel einer möglichen Studie
Ein Forschungsteam führt eine Studie durch, bei der eine trainingsbasierte Verbesserung der Gedächtnisleistung gemessen wird. Dazu wird der Intelligenzquotient von Studierenden vor dem Training erhoben. Da das Forscherteam jedoch keine Auskunft darüber hat, wie der IQ in der Stichprobe verteilt ist (wünschenswert wäre eine Normalverteilung), soll geprüft werden, ob der IQ in der Stichprobe normalverteilt ist.
Der zu analysierende Datensatz beinhaltet daher neben einer ID-Nummer für jeden Studierenden (ID) den IQ-Testwert (IQ).
Der Datensatz kann unter Quick Start heruntergeladen werden.
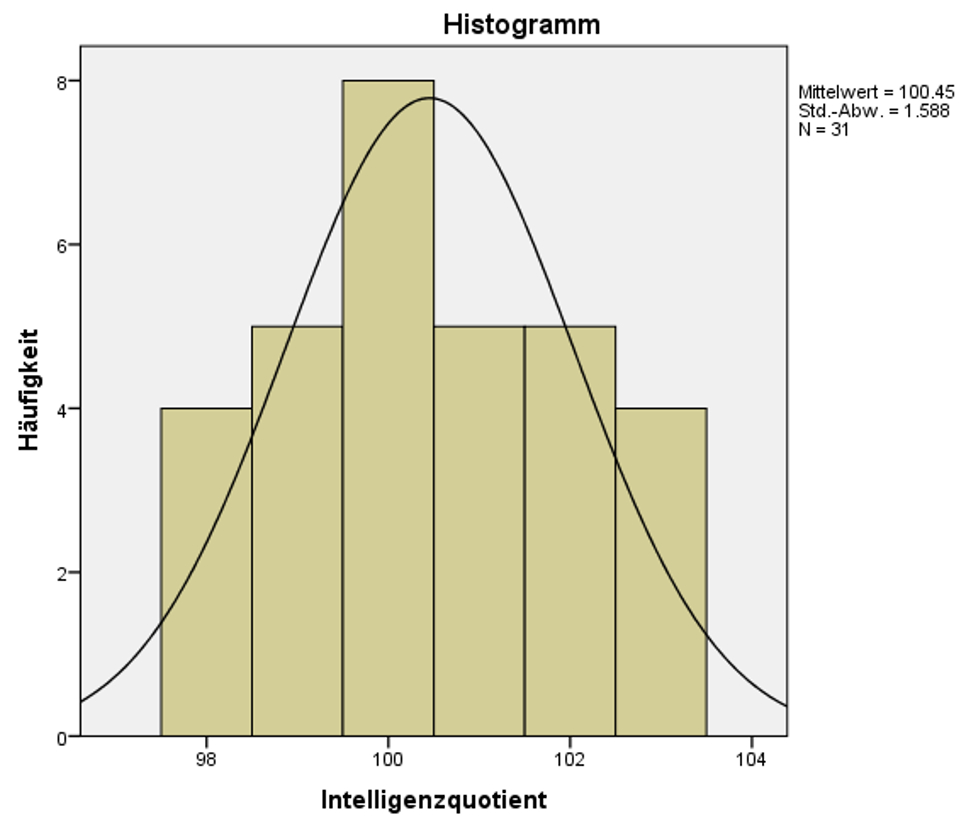
Wird ein Histogramm von IQ betrachtet (Abbildung 7), so ist erkennbar, dass es sich hierbei um eine Normalverteilung handeln könnte. Das Histogramm wird erzeugt über das SPSS-Menü Analysieren > Deskriptive Statistiken > Häufigkeiten.
3.4. Berechnung der Teststatistik
Grundsätzlich erfolgt die Berechnung auch im Falle des Tests auf Normalverteilung analog zum „einfachen“ Anpassungstest, ist jedoch ungleich aufwändiger. Daher soll aus Übersichtsgründen in diesem Beispiel darauf verzichtet werden.
3.5. SPSS-Befehle
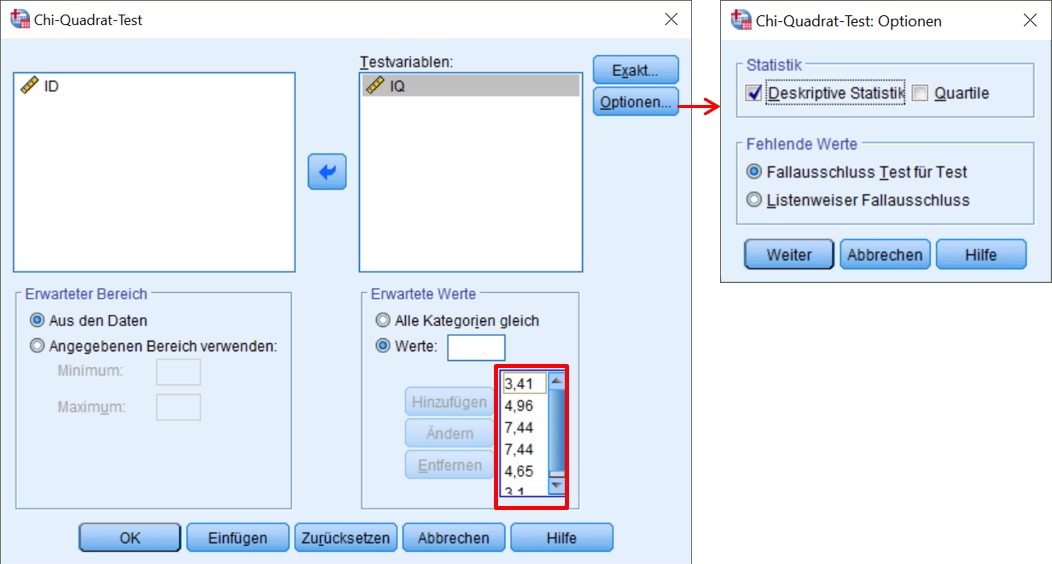
Hinweis
- Bei Erwartete Werte werden die erwarteten Häufigkeiten eingetragen
SPSS-Syntax
NPAR TESTS
/CHISQUARE=IQ
/EXPECTED=3.41 4.96 7.44 7.44 4.65 3.1
/STATISTICS DESCRIPTIVES
/MISSING ANALYSIS.
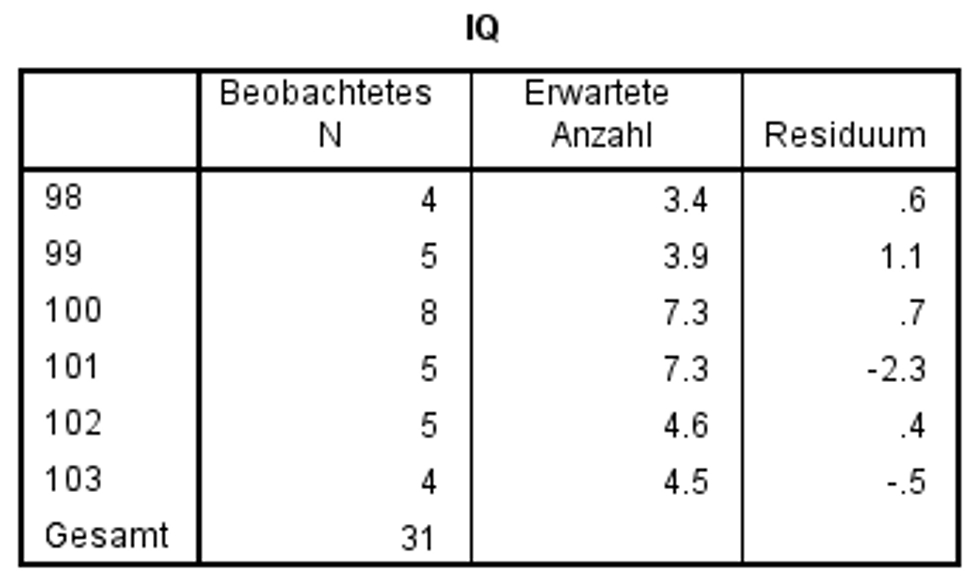
Abbildung 9 zeigt, dass die erwarteten Häufigkeiten für IQ = 98, IQ = 102 und IQ = 103 kleiner als 5 sind. Da bei zu geringen Zellbesetzungen – siehe Voraussetzungen – die Prüfgrösse nicht näherungsweise einer Chi-Quadrat-Verteilung folgt, sollte der Test eigentlich nicht verwendet werden. In diesem Falle könnte versucht werden, Kategorien zusammenzulegen, doch empfehlenswerter wäre es, eine grössere Stichprobe zu verwenden.
Abbildung 10 zeigt, dass der Test nicht signifikant ausfiele (p = .942), würde er dennoch interpretiert. Das hiesse, dass sich kein signifikanter Unterschied zwischen der beobachteten Verteilung und einer Normalverteilung zeigen würde. Entsprechend würde von einer Normalverteilung ausgegangen (Chi-Quadrat(5, n = 31) = 1.232, p = .942). Grundsätzlich ist beim Chi-Quadrat Test auf Normalverteilung ein nicht-signifikantes Ergebnis wünschenswert, wenn man normalverteilte Daten braucht.
3.7. Eine typische Aussage
Wären die Testvoraussetzungen erfüllt, so würde wie folgt berichtet: Die empirische Verteilung der IQ-Werte weicht nicht signifikant von einer Normalverteilung ab (Chi-Quadrat(5, n = 31) = 1.232, p = .942). Daher kann von einer Normalverteilung ausgegangen werden.
4. Kolmogorov-Smirnov-Test auf Normalverteilung
Eine Alternative zur Überprüfung, ob eine Normalverteilung vorliegt, ist der Kolmogorov-Smirnov-Test auf Normalverteilung (auch „KS-Anpassungstest“). Dieser Test ist empfehlenswert für den Datensatz „Chi-Quadrat-Test auf Normalverteilung“ unter Quick Start, denn er eignet sich für kleine Stichproben sowie auch für geringe Zellbesetzungen. Im Gegensatz zum Chi-Quadrat-Test gilt beim Kolmogorov-Smirnov-Test die Voraussetzung der Zellbesetzung ≥ 5 nicht.
4.1. Beispiele für mögliche Fragestellungen
- Ist der Intelligenzquotient in einer Schulklasse normalverteilt?
- Ist die Risikobereitschaft von jungen Männern normalverteilt?
- Folgen die Mathematiknoten einer Lehrabschlussprüfung einer Normalverteilung?
4.2. Voraussetzungen
| ✓ | Die Variable ist kontinuierlich (intervallskaliert) |
| ✓ | Nicht geeignet für grosse Stichproben, da sonst auch kleine Abweichungen von einer Normalverteilung signifikant ausfallen |
4.3. Berechnung der Teststatistik
Beim Kolmogorov-Smirnov-Test werden die einzelnen Testwerte mit normalverteilten Testwerten verglichen, die denselben Mittelwert und dieselbe Standardabweichung wie die erhobenen Daten zeigen. Auf eine Darstellung der Berechnungsweise wird an dieser Stelle verzichtet.
Es wird empfohlen, den Kolmogorov-Smirnov-Test lediglich bei kleineren Stichproben anzuwenden, da der Test bei grossen Stichproben fälschlicherweise signifikant ausfallen kann, obwohl sich die Verteilung nicht von einer theoretischen Normalverteilung unterscheidet.
4.4. SPSS-Befehle
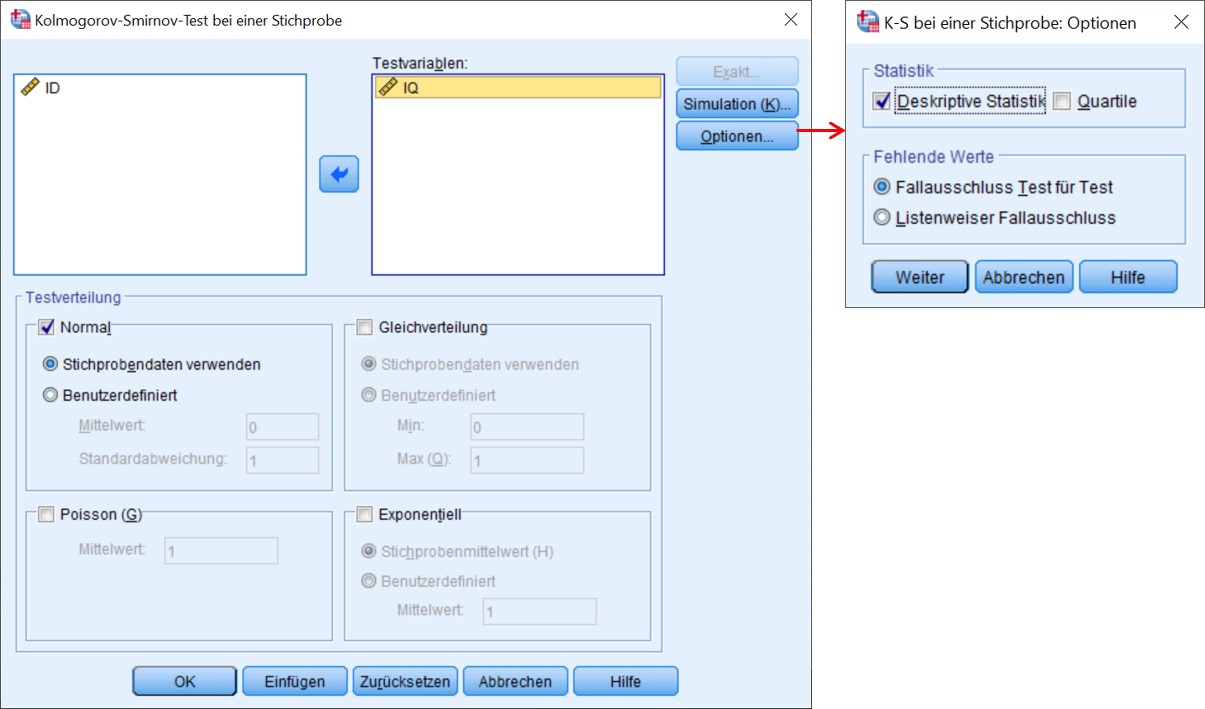
Hinweis
- Normal (= Normalverteilung) wird angeklickt, da herausgefunden werden soll, ob die Verteilung annähernd normal ist.
SPSS-Syntax
NPAR TESTS
/K-S(NORMAL)=IQ
/STATISTICS DESCRIPTIVES
/MISSING ANALYSIS.
Es zeigt sich, dass eine signifikante Abweichung von einer Normalverteilung vorliegt (da p < .05, siehe Abbildung 12). Es gibt einen signifikanten Unterschied zwischen der beobachteten Verteilung und einer Normalverteilung. Entsprechend kann nicht von einer Normalverteilung ausgegangen werden (Kolmogorov-Smirnov-Test, p = .041, n = 31).
Grundsätzlich ist auch beim Kolmogorov-Smirnov-Test ein nicht-signifikantes Ergebnis wünschenswert, wenn man normalverteilte Daten braucht.