 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen des Binomialtests
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Berechnung der Teststatistik
3. Der Binomialtest mit SPSS
3.1. SPSS-Befehle
3.2. Ergebnisse des Binomialtests
3.3. Eine typische Aussage
Quick Start
| Wozu wird der Binomialtest verwendet? Der Binomialtest testet, ob die Häufigkeitsverteilung einer dichotomen Variablen einer vermuteten Verteilung entspricht. SPSS-Menü
Analysieren > Nichtparametrische Tests > Klassische Dialogfelder > Binomial SPSS-Syntax
NPAR TESTS /BINOMIAL (0.50)=Variable /STATISTICS DESCRIPTIVES /MISSING ANALYSIS. SPSS-Beispieldatensatz
Binomial-Test |
1. Einführung
Der Binomialtest testet, ob die Häufigkeitsverteilung einer dichotomen Variablen einer vermuteten Verteilung entspricht.
Der Test wird bei dichotomen (= binären) Variablen angewandt, also bei Variablen mit nur zwei Ausprägungen (zum Beispiel 0 und 1, „Erfolg“ und „Misserfolg“, „gesund“ und „krank“, „trifft zu“ und „trifft nicht zu“ etc.).
Die Fragestellung des Binomialtests wird oft so verkürzt:
„Unterscheidet sich die beobachtete Auftretenswahrscheinlichkeit von der theoretisch erwarteten Auftretenswahrscheinlichkeit?“
1.1. Beispiele für mögliche Fragestellungen
- Wer entscheidet sich eher für ein bestimmtes Weichspülmittel? Frauen oder Männer?
- Kommt es beim Ausfüllen von Onlinesurveys zu mehr Abbrüchen, wenn ein Fortschrittsbalken verwendet wird oder wenn darauf verzichtet wird?
- Entspricht die Erkrankungsrate in einem bestimmten Land der von der Weltgesundheitsorganisation publizierten weltweiten Rate?
- Weist die Schweiz einen höheren, gleich hohen oder tieferen Anteil privater Computer mit dem Betriebssystem „Linux“ auf als der Durchschnitt der Europäischen Union?
1.2. Voraussetzungen des Binomialtests
| ✓ | Die Variable ist dichotom (sie hat nur zwei Ausprägungen) |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
Anlässlich einer Studie zum Thema „Powernap“ soll überprüft werden, ob nach einem Powernap eher nach etwas Süssem oder etwas Salzigem gegriffen wird. Daher werden im Rahmen der Studie 41 Probanden nach einem 30-minütigen Powernap gebeten, sich zwischen einem salzigen und einem süssen Snack zu entscheiden.
Der zu analysierende Datensatz enthält neben der Probandennummer (Proband) die Variable Testergebnis, welche den Wert 1 für Süsses und den Wert 2 für Salziges annimmt.
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Berechnung der Teststatistik
Der Binomialtest vergleicht eine empirisch gefundene Eintretenswahrscheinlichkeit mit einer theoretisch erwarteten Wahrscheinlichkeit. Die erwartete Wahrscheinlichkeit wird aufgrund von inhaltlichem Vorwissen festgelegt. Es kann ein beliebiger Wert angegeben werden, zum Beispiel 50%, aber auch 35% oder 82%. Im Rahmen der vorliegenden Beispielstudie ist die Nullhypothese, dass gleich häufig süsse wie salzige Snacks gewählt werden, also in 50% der Fälle. Daher wird eine relative Häufigkeit von 50% erwartet.
Die Zusammenstellung in Abbildung 1 lässt unschwer erkennen, dass häufiger süsse als salzige Snacks gewählt wurden, nämlich in 28 von 41 Fällen. Dies sind 68% der Fälle. Es stellt sich nun die Frage, ob sich dieser Wert signifikant von den in der Nullhypothese postulierten 50% unterscheidet.
Beim Binomialtest wird davon ausgegangen, dass es sich bei der untersuchten Variable – hier Testergebnis – um eine Zufallsvariable handelt. Es wird geprüft, ob die beobachtete relative Häufigkeit eines der beiden Ereignisse, der postulierten Auftretenswahrscheinlichkeit in der Grundgesamtheit entspricht. Im vorliegenden Beispiel wird geprüft, ob sich die beobachtete Wahrscheinlichkeit, dass Süsses gewählt wird (68%), von der erwarteten Auftretenswahrscheinlichkeit von 50% unterscheidet.
Die für diesen Test errechnete Teststatistik folgt einer Binomialverteilung. Daher wird der Test als „Binomialtest“ bezeichnet. Auf eine Darstellung der Berechnung wird an dieser Stelle verzichtet. Für weiterführende Informationen sei auf Statistiklehrbücher verwiesen.
3. Der Binomialtest mit SPSS
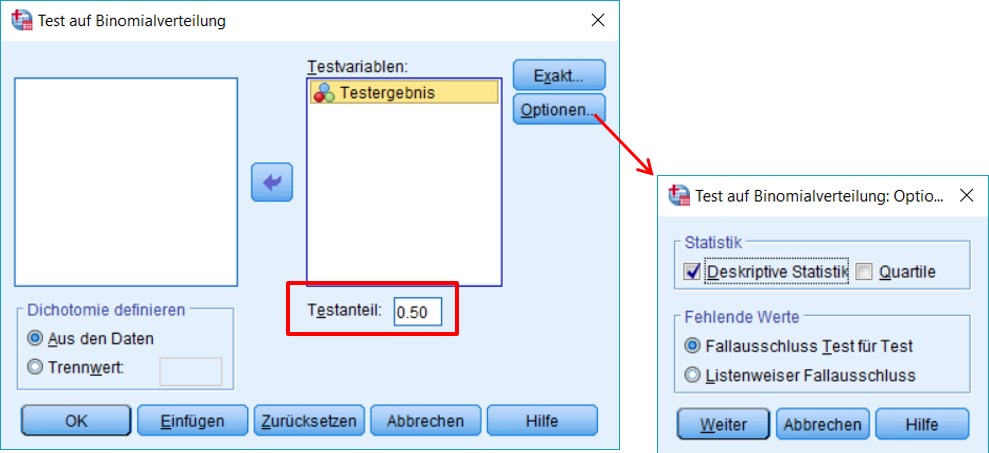
3.1. SPSS-Befehle
Hinweise
- Bei Testanteil wird die erwartete Wahrscheinlichkeit eingegeben (in unserem Beispiel 0.50 bzw. 50%).
- Werden mehrere Tests gleichzeitig berechnet, so muss entschieden werden, wie fehlende Werte behandelt werden sollen. Paarweiser Fallausschluss bedeutet, dass für jeden Test alle Fälle verwendet werden, die für beide Variablen gültige Werte aufweisen. Damit kann n je nach Variablenpaar unterschiedlich sein. Listenweiser Fallausschluss bedeutet, dass für alle Tests die gleichen Fälle verwendet werden – jene Fälle, die für alle Variablen in der Analyse gültige Fälle aufweisen.
SPSS-Syntax
NPAR TESTS
/BINOMIAL (0.50)=Testergebnis
/STATISTICS DESCRIPTIVES
/MISSING ANALYSIS.
3.2. Ergebnisse des Binomialtests
Deskriptive Statistiken
Hätten sich gleich viele Probanden für Süsses wie für Saures entschieden, so läge der Mittelwert bei 1.5 ((2+1)/2=1.5). Abbildung 3 zeigt jedoch, dass der Mittelwert bei 1.32 liegt und damit tendenziell Richtung Ausprägungskategorie 1 (Süsses) geht.
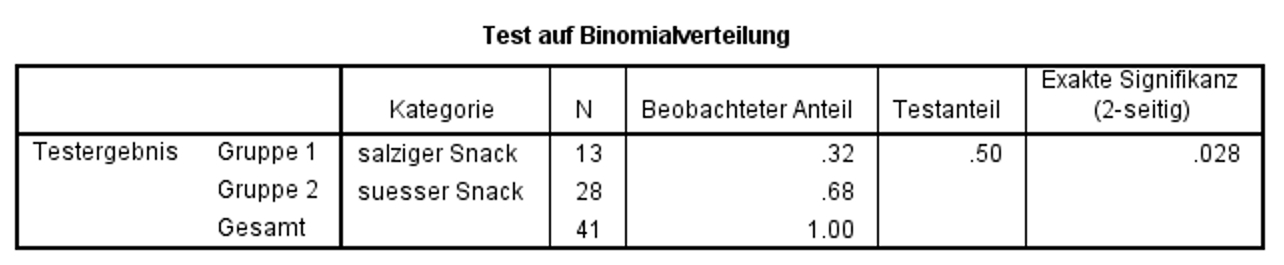
Binomialtest
Abbildung 4 zeigt das Ergebnis des Binomialtests, enthält aber auch einige nützliche deskriptive Angaben: 28 der 41 Probanden haben sich für den süssen Snack entschieden. Die beobachtete prozentuale Häufigkeit für den süssen Snack liegt also bei 28/41 bzw. 68% (siehe „Beobachteter Anteil“). Dieser Wert ist höher als der erwartete Wert von 0.5 (siehe „Testanteil“).
Die statistische Signifikanz dieses Unterschieds ist unter „Exakte Signifikanz (2-seitig)“ zu finden. Der p-Wert von .028 bedeutet, dass sich die beobachtete Häufigkeit und der erwartete Anteil signifikant unterscheiden (Exakter Binomialtest, zweiseitig, p = .028, n = 41).
3.3. Eine typische Aussage
Die Probanden wählten nach einem Powernap signifikant häufiger einen süssen als einen salzigen Snack (Exakter Binomialtest, zweiseitig, p = .028, n = 41).