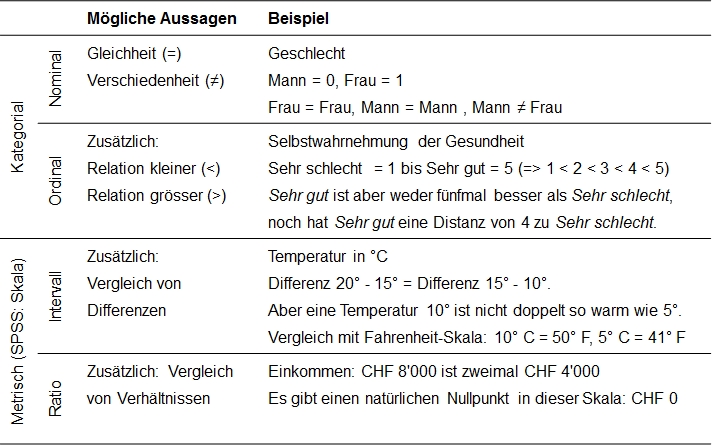
1. Die verschiedenen Skalenniveaus
1.1. Nominalskala
1.2. Ordinalskala
1.3. Intervallskala
1.4. Ratioskala
2. Hierarchie der Skalenniveaus
3. Skalenniveau und SPSS
1. Die verschiedenen Skalenniveaus
Neben dem Ziel der Untersuchung ist auch die Qualität der Daten ausschlaggebend für die Wahl der Analysemethode. Die verschiedenen Methoden unterscheiden sich darin, welches Skalenniveau die verwendeten Variablen aufweisen müssen. Auf dieser Seite werden die Skalenniveaus sowie ihre Bezeichnungen in SPSS kurz vorgestellt.
1.1. Nominalskala
Nominalskalierte Daten haben den niedrigsten Informationsgehalt. Es handelt sich meist um Kategorien, die zur Auswertung numerisch codiert werden. Sie werden daher manchmal auch „Kategorialskalen“ genannt. Beispiele hierfür sind Geschlecht (1 für männlich, 2 für weiblich) oder Wohnort (1 für Zürich, 2 für Bern, 3 für Basel). Bei nur zwei Merkmalsausprägungen spricht man auch von einer dichotomen oder binären Variablen. Da die Zahlenwerte selbst gewählt werden können, sind sie an sich nicht bedeutsam, sondern arbiträr: So könnte 1 auch für weiblich und 2 für männlich gewählt werden. Mit nominalskalierten Daten lassen sich keine Rechenoperationen (Addition, Subtraktion usw.) durchführen, sondern nur Aussagen über Häufigkeiten machen.
Beispielfrage:
1.2. Ordinalskala
Ordinalskalierte Daten folgen einer Rangreihe. Statt „Ordinalskala“ wird daher auch der Ausdruck „Rangskala“ verwendet. Es lassen sich keine Aussagen über die absoluten Abstände zwischen den Werten machen. Ein Beispiel für ordinalskalierte Daten sind Schulnoten. Im Schweizer System ist eine 6 klar besser als eine 3, aber es lässt sich keine numerische Aussage darüber machen, wie viel besser die 6 genau ist. Sie ist nicht doppelt so gut wie eine 3. Auch bedeutet der Abstand zwischen einer 1 und einer 2 nicht das Gleiche, wie der Abstand zwischen einer 4 und einer 5. Mit ordinalskalierten Variablen lassen sich keine Rechenoperationen (Addition, Subtraktion usw.) durchführen.
Eine besonders häufig anzutreffende Ordinalskala ist die Likert-Skala (auch „Ratingskala“, siehe Abbildung 2).
Auf einer Likert-Skala drücken die Werte von tief bis hoch (z.B. 0 bis 5, 1 bis 7) eine Abstufung der Intensität dar – zum Beispiel von „stimme überhaupt nicht zu“ bis zu „stimme voll und ganz zu“ oder von „sehr unglücklich“ bis „sehr glücklich“.
1.3. Intervallskala
Bei intervallskalierten Merkmalen lässt sich auch eine Aussage über die absoluten Abstände zwischen den Werten machen. Ein Beispiel hierfür ist die Temperatur in Grad Celsius. Der Abstand zwischen -15 und 4 Grad ist genauso gross wie der zwischen 14 und 33 Grad. Allerdings ist auch hier darauf zu achten, dass 40 Grad nicht doppelt so warm wie 20 Grad sind, da die Temperaturskala einen willkürlich festgelegten Nullpunkt hat (den Gefrierpunkt des Wassers).
1.4. Ratioskala
Ratioskalierte Merkmale haben anders als intervallskalierte Merkmale einen natürlich gegebenen Nullpunkt. Beispiele für ratioskalierte Merkmale sind Alter, Einkommen oder Grösse. Andere Bezeichnungen für eine Ratioskala sind „Verhältnis-“ oder „Proportionalskala“. Sind Merkmale ratioskaliert, so lassen sich auch Aussagen über die Verhältnisse der Merkmalsausprägungen machen. So ist jemand, der 1,80 cm gross ist, tatsächlich doppelt so gross wie ein 90 cm grosses Kind. Auch die Temperatur in Kelvin ist ratioskaliert, da der Nullpunkt dem physikalischen absoluten Nullpunkt entspricht.
2. Hierarchie der Skalenniveaus
Die Nominalskala ist die „niedrigste“ und die Ratioskala die „höchste“ Skala. Je höher das Skalenniveau ist, desto umfangreichere und präzisere Aussagen lassen sich über die Variablen machen. Dabei schliesst ein höheres Skalenniveau auch immer die Eigenschaften der niedrigeren mit ein (vergleiche Abbildung 3), so dass Daten auch auf einem niedrigeren Niveau interpretiert werden können. Eine Skala eines höheren Niveaus kann also als Skala eines niedrigeren Niveaus behandelt werden, aber nicht umgekehrt (Beispiel: Auf der Basis des Alters in Jahren (Ratioskala) kann eine binäre Variable darüber erstellt werden, ob jemand minderjährig ist (Nominalskala), aber umgekehrt nicht). Wünschenswert ist es deshalb, möglichst alle Daten auf Intervallskalenniveau zu erheben.
In der sozialwissenschaftlichen Forschung ist es nicht immer möglich oder sehr aufwändig, ein hohes Skalenniveau zu erreichen (z.B. bei Einkommen). Oft lässt sich das Skalenniveau eines Messinstrumentes auch unterschiedlich interpretieren. Ein Beispiel hierfür sind Items, die auf einer Likert-Skala gemessen werden. Grundsätzlich müssten Antworten auf einer Likert-Skala als ordinalskaliert betrachtet werden, denn es kann nicht zwingend davon ausgegangen werden, dass die Teilnehmer einer Umfrage die Abstände zwischen den Antworten als gleich wahrnehmen. Trotzdem werden solche Items in der Praxis oft als intervallskaliert behandelt, wenn die Annahme plausibel erscheint.
3. Skalenniveau und SPSS
Es ist wichtig, dass man sich vor der Datenanalyse mit SPSS über das Skalenniveau der Daten sicher ist, da alle Variablen in SPSS zunächst automatisch als metrisch eingstuft werden. Daher sollte als erstes in der Variablenansicht das Skalenniveau der Daten richtig eingestellt werden. SPSS unterscheidet hierbei nicht zwischen intervall- oder ratioskaliert, so dass man nur „Skala“ auswählen kann. Dass heisst, SPSS fasst Intervallskalen und Ratioskalen unter dem Begriff „Skala“ zusammen. Mit SPSS lassen sich deshalb teilweise Methoden anwenden, für welche die Daten eigentlich nicht das richtige Skalenniveau aufweisen.