Zu Beginn eines Forschungsprojektes muss zunächst bestimmt werden, was die Art der Fragestellung ist. Je nach Typ der Fragestellung kommen neben deskriptiven Analysen zwei Arten der Analyse zum Einsatz: Dependenzanalysen und Interdependenzanalysen.
1. Einleitung
2. Unterschiede
3. Zusammenhänge
1. Einleitung
Unter Dependenzanalysen werden Verfahren verstanden, mit denen Strukturen überprüft werden sollen. Zu diesen Verfahren gehören beispielsweise die Varianzanalyse, Regressionsanalyse, Diskriminanzanalyse, t-Tests, Chi-Quadrat-Tests etc. Ziel der Analysen ist es, Abhängigkeiten (Dependenzen) zwischen „abhängigen“ und „unabhängigen“ Variablen zu untersuchen. Entsprechend werden die Variablen daher vor Anwendung der entsprechenden Methode in abhängige (zu erklärende) und unabhängige (erklärende) Variablen aufgeteilt. Diese Einteilung lässt sich meist durch entsprechende Fachliteratur oder anhand von früheren Ergebnissen begründen. Je nach Ziel der Untersuchung und anhand des Skalenniveaus der Variablen lassen sich die Verfahren noch weiter aufteilen. Je nach Art der Forschungsfrage und Hypothesen werden Unterschiede oder Zusammenhänge zwischen Variablen untersucht.
Das Ziel einer Dependenzanalyse ist es, statistische Aussagen über einen bestimmten Sachverhalt zu machen. Hierzu müssen eine zu prüfende Hypothese, genannt Nullhypothese (H0), und die Gegen- oder Alternativhypothese (H1) aufgestellt werden. Da es in den meisten Fällen nicht möglich ist, die komplette Grundgesamtheit (z.B. alle Schüler der Schweiz) zu befragen, wird aus der Grundgesamtheit eine Stichprobe (z.B. 1’200 Schüler) gezogen. Mit dieser Stichprobe soll nun eine Aussage über die Grundgesamtheit gemacht werden.
Um die Hypothesen zu überprüfen, werden sogenannte Signifikanztests verwendet. Alle Methoden, die unter Dependenzanalysen aufgeführt sind, sind solche Tests, was bedeutet, dass sich mit diesen Methoden überprüfen lässt, ob die erhobenen Unterschiede oder Zusammenhänge statistisch signifikant sind. Da diese Aussagen nur anhand von Stichproben gemacht werden, lassen sich die Hypothesen über die Grundgesamtheit nur mit einer vorher festgelegten Wahrscheinlichkeit annehmen oder verwerfen.
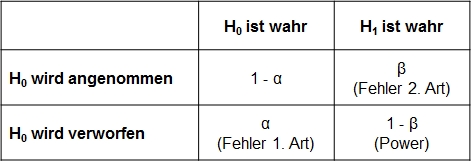
Bei der Entscheidung, ob eine Hypothese angenommen wird oder nicht, können zwei Fehler gemacht werden: In der Grundgesamtheit ist H0 wahr, aufgrund der Daten der Stichprobe wird die Hypothese aber verworfen. Dieser Fehler wird Fehler 1. Art oder α-Fehler genannt. Andererseits könnte in der Grundgesamtheit aber auch H1 wahr sein, fälschlicherweise wird aber H0 angenommen. Dieser Fehler wird Fehler 2. Art oder β-Fehler genannt. Abbildung 1 gibt einen Überblick über die verschiedenen Möglichkeiten und Fehlerarten:
Abbildung 1: Fehlerarten bei der Hypothesenprüfung
Die Wahrscheinlichkeit, bei einer Entscheidung einen Fehler 1. Art zu begehen, wird als Signifikanzniveau α oder Irrtumswahrscheinlichkeit bezeichnet. Das Signifikanzniveau hängt unter anderem auch von der Stichproben- und Grundgesamtheitsgrösse ab. In Abhängigkeit von der Stichprobengrösse und davon, welche Art Fehler vermieden werden soll, sollte das Signifikanzniveau vor Beginn der Untersuchung festgelegt werden. Bei sozialwissenschaftlichen Forschungen wird meistens ein Signifikanzniveau von 5% oder 1%, selten auch von 10% vorausgesetzt. Sind die Folgen einer Fehlentscheidung allerdings gravierend (z.B. bei Medikamententests) sollte das Niveau niedriger angesetzt werden.
SPSS gibt bei allen Methoden das berechnete Signifikanzniveau als Zahl aus – das ist der sogenannte p-Wert. Bei einem festgelegten Signifikanzniveau von 5% sollte dieser Wert unter 0.05 liegen. Dann lässt sich sagen, dass mit einer Wahrscheinlichkeit von mehr als 95% davon ausgegangen werden kann, dass die Varianz der Daten nicht zufällig entstanden ist.
2. Unterschiede
Mit einer grossen Anzahl von Methoden lassen sich die Unterschiede zwischen zwei oder mehr Variablen untersuchen. Anhand der gesammelten Daten kann überprüft werden, ob diese Unterschiede auch statistisch signifikant sind. Je nachdem, was für Unterschiede gemessen werden sollen, müssen andere Verfahren gewählt werden. Unterschiede
3. Zusammenhänge
Viele verschiedene Methoden können genutzt werden, um Zusammenhänge zwischen zwei oder mehr Variablen zu untersuchen. Neben der Anzahl an Variablen unterschieden sich die Verfahren noch in den Voraussetzungen, welche die zu untersuchenden Daten erfüllen müssen. Zusammenhänge