Zur Untersuchung von Zusammenhängen werden auf dieser Seite insgesamt sechs Verfahren besprochen. Mit vier von ihnen können die Zusammenhänge zwischen zwei Variablen untersucht werden, mit den zwei anderen können auch mehr Variablen untersucht werden. Neben der Menge der Variablen unterscheiden sich diese Methoden bezüglich der Voraussetzungen.
1. Zwei Variablen
Mit den folgenden vier Methoden lässt sich der Zusammenhang zwischen zwei Variablen untersuchen: Pearson Chi-Quadrat-Test (Kontingenzanalyse), Rangkorrelation nach Spearman, Korrelation nach Bravais und Pearson und einfache Regression.
1.1. Korrelation nach Bravais und Pearson
Ist der vermutete lineare Zusammenhang zweier intervallskalierter Merkmale ungerichtet, kann die Korrelation nach Bravais und Pearson (auch „Pearson Korrelation“) zwischen diesen zwei Variablen berechnet werden. „Ungerichtet“ bedeutet, dass beide Variablen gemeinsam variieren, jedoch nicht gesagt werden kann, dass eine Variable durch die andere bedingt wird. Ein Beispiel hierfür könnte der folgende Zusammenhang sein:
Abbildung 1: Beispiel Korrelation nach Bravais und Pearson
Einerseits könnte angenommen werden, dass je höher jemand motiviert ist, desto erfolgreicher er auch ist. Andererseits kann aber auch Erfolg dazu führen, dass jemand noch motivierter an seine Aufgaben geht. Eine unabhängige bzw. abhängige Variable kann nicht bestimmt werden.
Korrelation nach Bravais und Pearson
1.2. Einfache Regression
Ist der vermutete lineare Zusammenhang zweier intervallskalierter Merkmale gerichtet, kann eine einfache Regressionsanalyse durchführt werden. Im Falle einer gerichteten Hypothese wird angenommen, dass eine Variable durch die andere bedingt wird. Dies wird deutlich an folgendem Beispiel:
Abbildung 2: Beispiel einfache Regression
Es kann plausibel begründet werden, dass die Intelligenz eines Kindes die Schulnoten beeinflusst, weniger plausibel ist es jedoch, dass die Schulnoten die Intelligenz beeinflussen. Einfache Regression
1.3. Rangkorrelation nach Spearman
Handelt es sich bei zwei Variablen um ordinalskalierte Merkmale, so lässt sich der Rangkorrelationskoeffizient von Spearman berechnen. Beispielsweise kann mit dem Rangkorrelationskoeffizient überprüft werden, ob die Leistung in einem Rechentest die Schüler einer Klasse in dieselbe Reihenfolge einteilt wie die Beurteilung der Leistung durch den Lehrer.
Abbildung 3: Beispiel Rangkorrelation nach Spearman
1.4. Pearson Chi²-Test
Der Zusammenhang zwischen zwei nominal- bis ordinalskalierten Merkmalen lässt sich mittels eines Pearson Chi-Quadrat-Tests (auch „Kontingenzanalyse“) untersuchen. Die beiden untersuchten Variablen werden in einer sogenannten „Kreuztabelle“ gegeneinander tabelliert. Die beobachteten Häufigkeiten werden mit den erwarteten Häufigkeiten, gegeben die beiden Merkmale hängen nicht zusammen, verglichen. Beispielsweise kann so der Zusammenhang zwischen Geschlecht und Studienfachwahl untersucht werden.
Abbildung 4: Beispiel Pearson Chi-Quadrat-Test
2. Mehr als zwei Variablen
Mit den folgenden Methoden lassen sich Zusammenhänge zwischen mehreren unabhängigen Variablen und einer abhängigen Variablen überprüfen: die multiple Regression (bei einer intervallskalierten abhängigen Variablen) und die logistische Regression (bei einer dichotomen abhängigen Variablen). Daneben gibt es Erweiterungen dieser Modelle für nominale und ordinale abhängige Variablen.
2.1. Multiple Regression
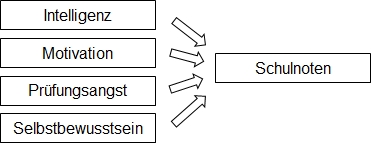
Mittels einer multiplen Regression kann der Zusammenhang zwischen einer intervallskalierten abhängigen Variablen und mehreren intervallskalierten oder als Dummy codierten unabhängigen Variablen untersucht werden. Beispielsweise könnte der Einfluss von Intelligenz, Motivation, Prüfungsangst und Selbstbewusstsein auf Schulnoten untersucht werden.
Abbildung 5: Beispiel multiple Regression
2.2. Logistische Regression
Mittels einer logistischen Regression kann die Eintrittswahrscheinlichkeit einer dichotomen abhängigen Variablen in Abhängigkeit von unabhängigen Variablen untersucht werden. „Dichotom“ ist gleichbedeutend mit „binär“: Die Variable hat nur zwei Ausprägungen, z.B. 0 und 1. Ein Beispiel für eine Problemstellung, die mit dieser Methode untersucht werden kann, ist folgende:
Abbildung 6: Beispiel logistische Regression
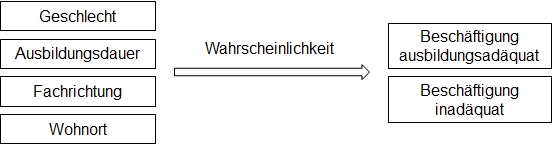
Es soll untersucht werden, wie das Geschlecht, die Ausbildungsdauer, die Fachrichtung und der Wohnort die Wahrscheinlichkeit beeinflussen, ob ein Absolvent sich ein Jahr nach Abschluss in einer ausbildungsadäquaten oder -inadäquaten Position befindet.
Logistische Regression