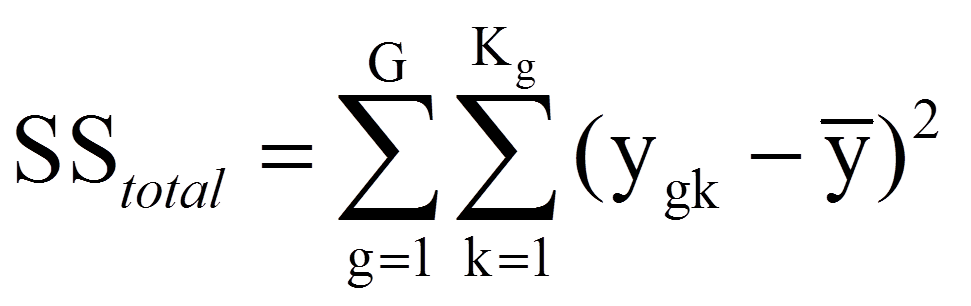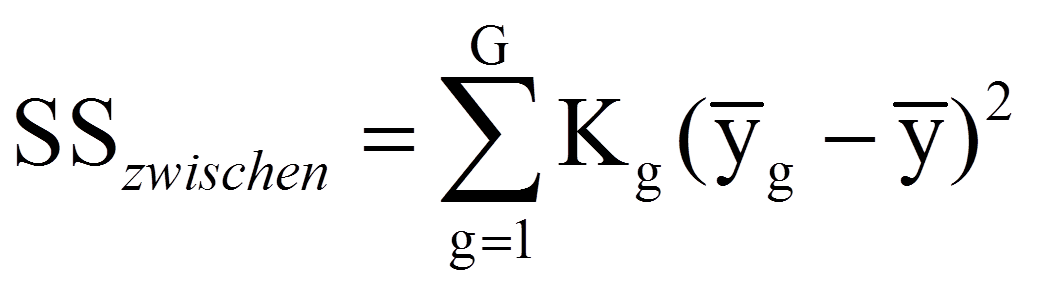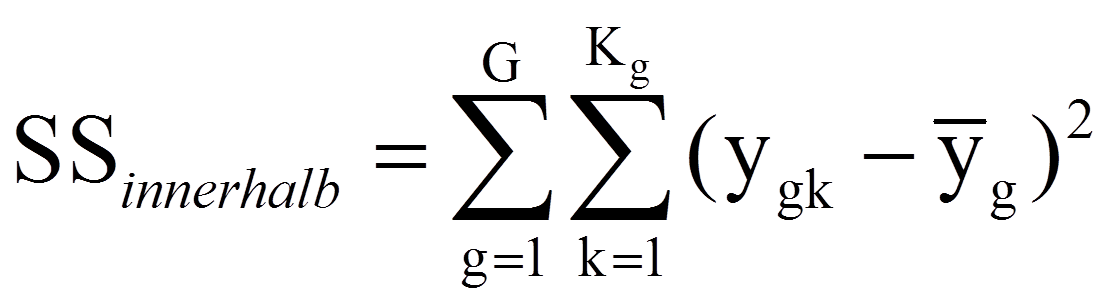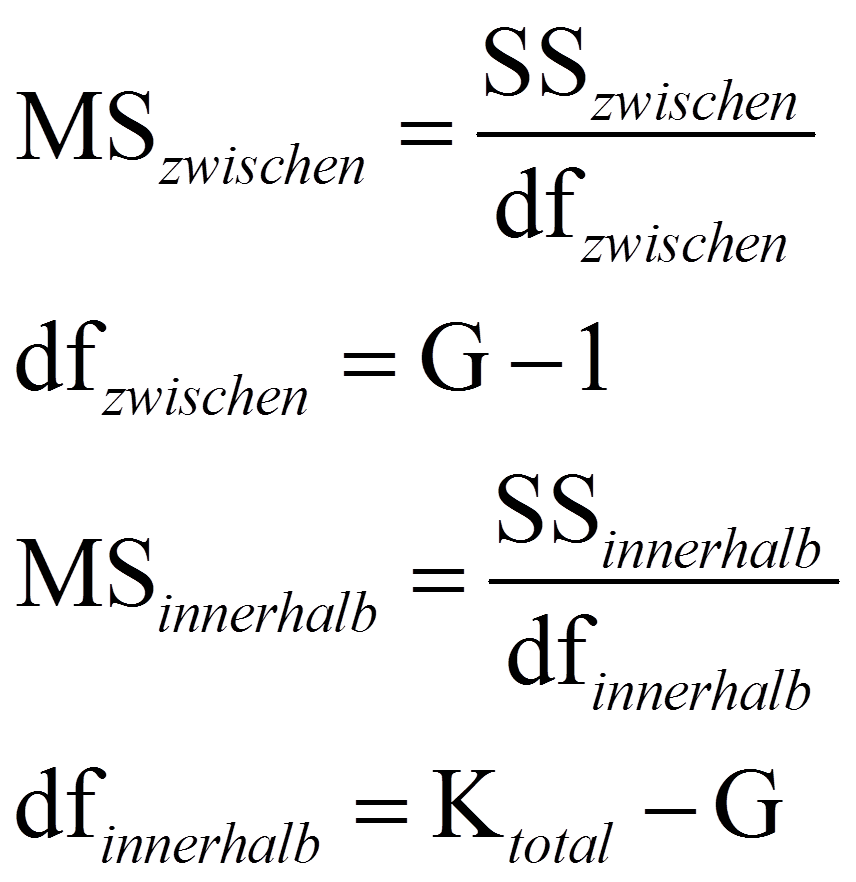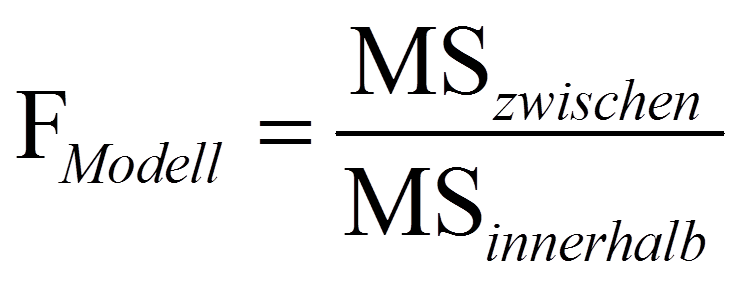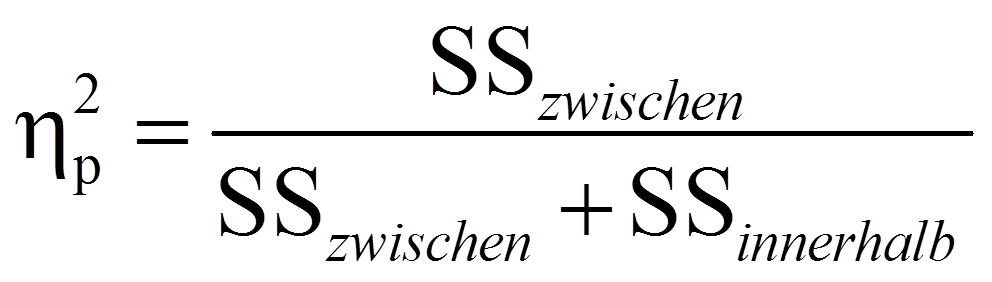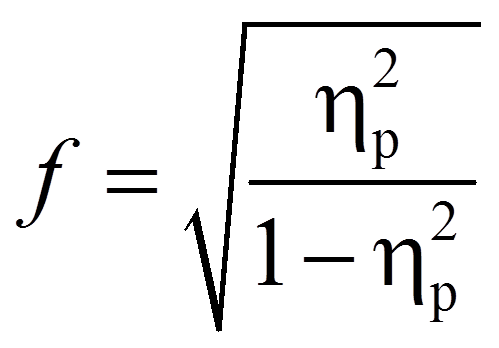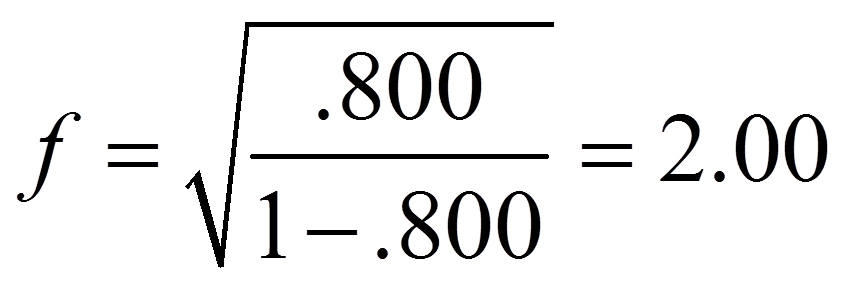 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen der einfaktoriellen Varianzanalyse
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Die Grundidee der Varianzanalyse
2.3. Berechnung der Teststatistik
3. Die einfaktorielle Varianzanalyse mit SPSS
3.1. SPSS-Befehle
3.2. Boxplots zur Illustration
3.3. Prüfung der Varianzhomogenität (Levene-Test)
3.4. Ergebnisse der einfaktoriellen Varianzanalyse
3.5. Post-hoc-Tests
3.6. Profildiagramm
3.7. Berechnung der Effektstärke
3.8. Eine typische Aussage
Quick Start
| Wozu wird die einfaktorielle Varianzanalyse verwendet? Die einfaktorielle Varianzanalyse testet, ob sich die Mittelwerte mehrerer unabhängiger Gruppen (oder Stichproben) unterscheiden, die durch eine kategoriale unabhängige Variable definiert werden. SPSS-Menü
Analysieren > Allgemeines lineares Modell > Univariat SPSS-Syntax
UNIANOVA abhängige Variable BY Faktor /METHOD=SSTYPE(3) /INTERCEPT=INCLUDE /POSTHOC= Faktor (BONFERRONI) /PRINT=HOMOGENEITY DESCRIPTIVE /CRITERIA=ALPHA(.05) SPSS-Beispieldatensatz
Einfaktorielle Varianzanalyse ohne Messwiederholung |
1. Einführung
Die einfaktorielle Varianzanalyse – auch „einfaktorielle ANOVA“, da in Englisch „Analysis of Variance“ – testet, ob sich die Mittelwerte mehrerer unabhängiger Gruppen (oder Stichproben) unterscheiden, die durch eine kategoriale unabhängige Variable definiert werden. Diese kategoriale unabhängige Variable wird im Kontext der Varianzanalyse als „Faktor“ bezeichnet. Entsprechend werden die Ausprägungen der unabhängigen Variable „Faktorstufen“ genannt, wobei auch der Begriff der „Treatments“ gebräuchlich ist. Als „einfaktoriell“ wird eine Varianzanalyse bezeichnet, wenn sie lediglich einen Faktor, also eine Gruppierungsvariable, verwendet.
Das Prinzip der Varianzanalyse besteht in der Zerlegung der Varianz der abhängigen Variable. Die Gesamtvarianz setzt sich aus der sogenannten „Varianz innerhalb der Gruppen“ und der „Varianz zwischen den Gruppen“ zusammen. Diese beiden Anteile werden im Rahmen einer Varianzanalyse miteinander verglichen. Die einfaktorielle ANOVA stellt eine Verallgemeinerung des t-Tests für unabhängige Stichproben für den Vergleich von mehr als zwei Gruppen (oder Stichproben) dar. Die Fragestellung der einfaktoriellen Varianzanalyse wird oft so verkürzt: „Unterscheiden sich die Mittelwerte einer abhängigen Variable zwischen mehreren Gruppen? Welche Faktorstufen unterscheiden sich?“
1.1. Beispiele für mögliche Fragestellungen
- Unterscheiden sich stark, moderat und geringfügig emotionale Menschen bezüglich der Menge des Stresshormons Cortisol im Blut?
- Beeinflusst der Kohlendioxidgehalt (sehr tief, tief, mittel, hoch, sehr hoch) das Wachstum von Birken?
- Werden bei Konsumenten nach einer Degustation von fünf Traubensorten unterschiedlich hohe Zahlungsbereitschaften für die verschiedenen Sorten gemessen?
- Mit vier Gruppen von Versuchspersonen wurde je ein anderes Gedächtnistraining durchgeführt. Welches der Gedächtnistrainings ist das erfolgreichste in Bezug auf die anschliessend gemessene Gedächtnisleistung?
1.2. Voraussetzungen der einfaktoriellen Varianzanalyse
| ✓ | Die abhängige Variable ist intervallskaliert |
| ✓ | Die unabhängige Variable (Faktor) ist kategorial (nominal- oder ordinalskaliert) |
| ✓ | Die durch den Faktor gebildeten Gruppen sind unabhängig |
| ✓ | Die abhängige Variable ist normalverteilt innerhalb jeder der Gruppen (Ab > 25 Probanden pro Gruppe sind Verletzungen in der Regel unproblematisch) |
| ✓ | Homogenität der Varianzen: Die Gruppen stammen aus Grundgesamtheiten mit annähernd identischen Varianzen der abhängigen Variablen (siehe Levene-Test) |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
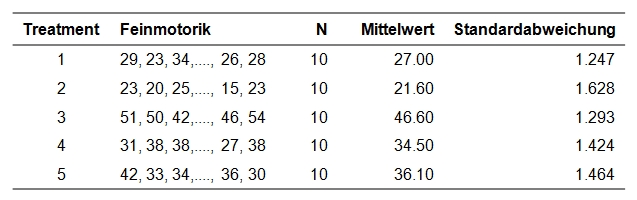
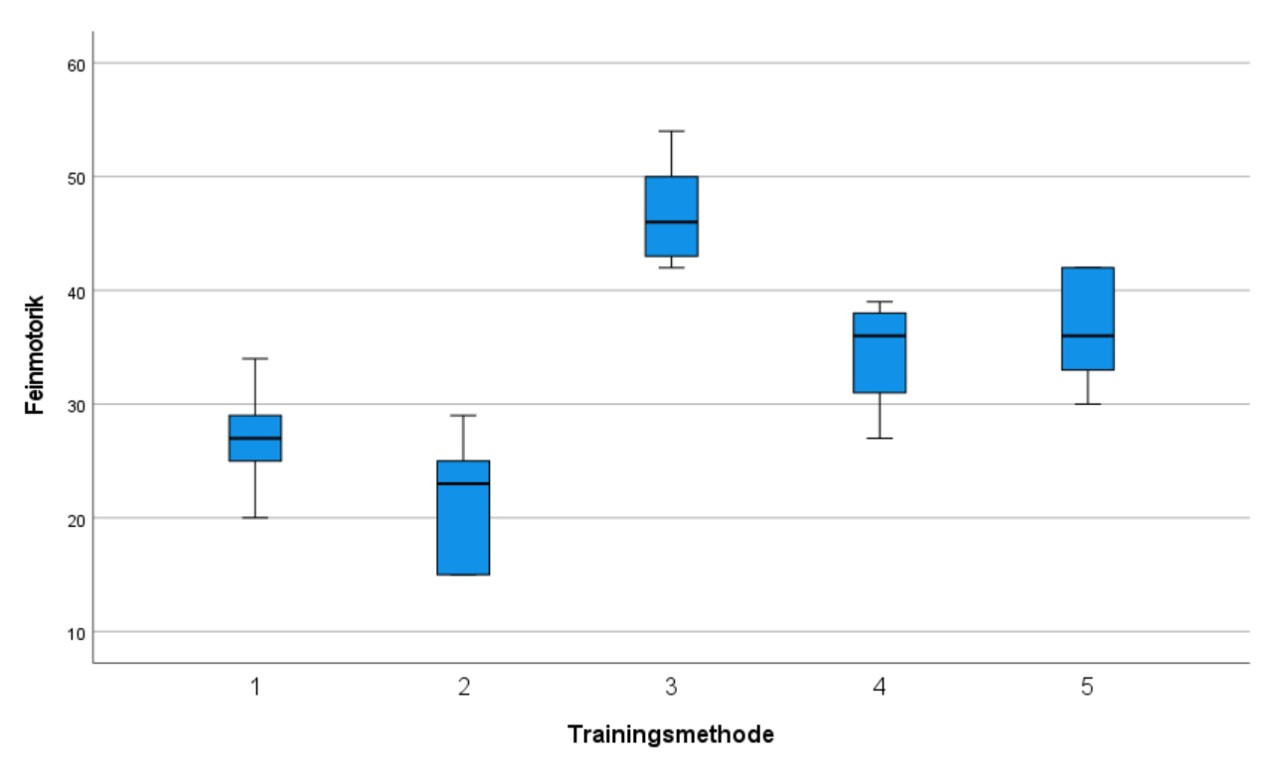
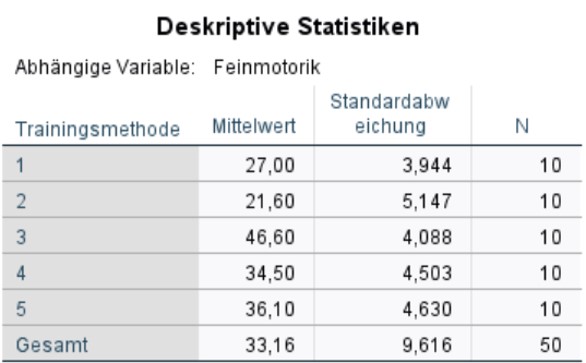
50 Senioren wurden zufällig fünf Gruppen zugeteilt, mit denen je eines von fünf verschiedenen motorischen Trainings durchgeführt wurde. Danach wurde die feinmotorische Kontrolle der Probanden erhoben. Es soll nun beantwortet werden, welche der fünf Trainingsmethoden sich am effektivsten auf die feinmotorische Kontrolle auswirkt.
Der zu analysierende Datensatz enthält neben einer Probandennummer (ID) die Gruppierungsvariable TrMe, welche je nach Treatment einen Wert zwischen 1 und 5 annimmt, und die Variable Feinm, die den Messwert für die Feinmotorik enthält.
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Die Grundidee der Varianzanalyse
Ein Blick auf die Gruppenmittelwerte der Beispieldaten (Abbildung 1) zeigt, dass sich die Mittelwerte unterscheiden. Um zu überprüfen, ob die Unterschiede signifikant sind, wird eine Varianzanalyse durchgeführt.
Zerlegung der individuellen Messwerte
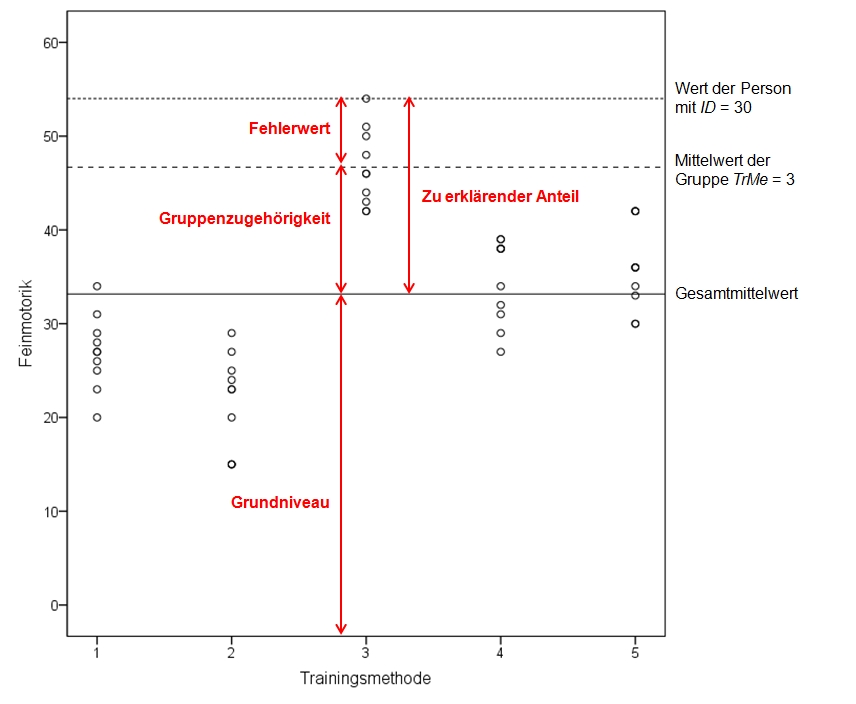
Die Varianzanalyse ist daran interessiert, die Unterschiede zwischen den beobachteten Werten und dem Gesamtmittelwert der Stichprobe zu erklären. Die Grundidee ist, dass jeder Messwert in drei Anteile zerlegt werden kann (siehe Abbildung 2):
- „Grundniveau“: Dies ist der Mittelwert der gesamten Stichprobe (ungeachtet der Gruppenzugehörigkeit), der sogenannte „Gesamtmittelwert“. Im Beispiel ist dieses Ausgangsniveau der Gesamtmittelwert von Feinm. Dieser ist für die Berechnung der Varianzanalyse zwar wichtig, doch die Varianzanalyse versucht nicht, diesen Gesamtmittelwert zu erklären.
- Effekt der Gruppenzugehörigkeit: Dieser Anteil repräsentiert die Gruppenzugehörigkeit und entspricht der Differenz zwischen dem Gesamtmittelwert und dem jeweiligen Gruppenmittelwert. Im vorliegenden Beispiel hat jede Gruppe an einem unterschiedlichen Training teilgenommen. Wirken sich diese Treatments unterschiedlich auf die Feinmotorik aus, so erklären die Treatments einen Teil der Abweichung der Messwerte vom Gesamtmittelwert. Es wird hierbei von einem „Haupteffekt“ der Variable TreMe gesprochen, also der direkten Auswirkung des Faktors auf die abhängige Variable.
- Fehlerwert: Dieser Anteil umfasst Messfehler und alle individuellen Abweichungen vom Gesamtmittelwert ein, die nicht durch die Gruppenzugehörigkeit erklärt werden können. Im vorliegenden Beispiel kann davon ausgegangen werden, dass bereits vor der Studie Unterschiede bezüglich der feinmotorischen Fähigkeiten vorgelegen haben. Zusätzlich könnten auch noch individuelle Unterschiede in der erlebten Wirksamkeit der Trainings vorliegen.
Quadratsummen
Eine Varianzanalyse versucht, die Abweichungen der individuellen Werte vom Gesamtmittelwert zu erklären (siehe Abbildung 2). Als Mass für die zu erklärenden Abweichungen aller Personen werden alle individuellen Abweichungen vom Gesamtmittelwert quadriert und aufsummiert. Dies führt zur Gesamtquadratsumme SStotal (da engl. „Sum of Squares“):
mit
| = | Laufindex der Gruppen von 1 bis G (im vorliegenden Beispiel: G = 5 Gruppen) | |
| = | Laufindex der Individuen innerhalb einer Gruppe von 1 bis Kg (hier: K1 = K2 = K3 = K4 = K5 = 10, Ktotal= 50) |
Diese Quadratsumme wird im Rahmen der Varianzanalyse in zwei Teile zerlegt: Das, was durch die Gruppenzugehörigkeit erklärt werden kann, und das, was nicht erklärt werden kann. Das erstere ist die Quadratsumme zwischen den Gruppen SSzwischen und basiert auf dem Unterschied zwischen den Gruppenmittelwerten und dem Gesamtmittelwert:
2.3. Berechnung der Teststatistik
Zur Berechnung der Teststatistik F werden die mittleren Quadratsummen MSzwischen und MSinnerhalb benötigt („MS“ da engl. „mean squares“). Dazu werden die Quadratsummen durch ihre jeweiligen Freiheitsgrade dividiert:
Signifikanz der Teststatistik
Je mehr Variation durch die Gruppenzugehörigkeit erklärt wird, desto höher fällt der F-Wert aus (da MSzwischen ein Mass für die erklärte Varianz darstellt, während MSinnerhalb ein Mass für die Residualvarianz des Modells darstellt). Dieser F-Wert wird mit dem kritischen Wert auf einer durch die Freiheitsgrade dfzwischen und dfinnerhalb charakterisierten F-Verteilung verglichen. Ist der F-Wert höher als der kritische Wert, so ist der Test signifikant.
3. Die einfaktorielle Varianzanalyse mit SPSS
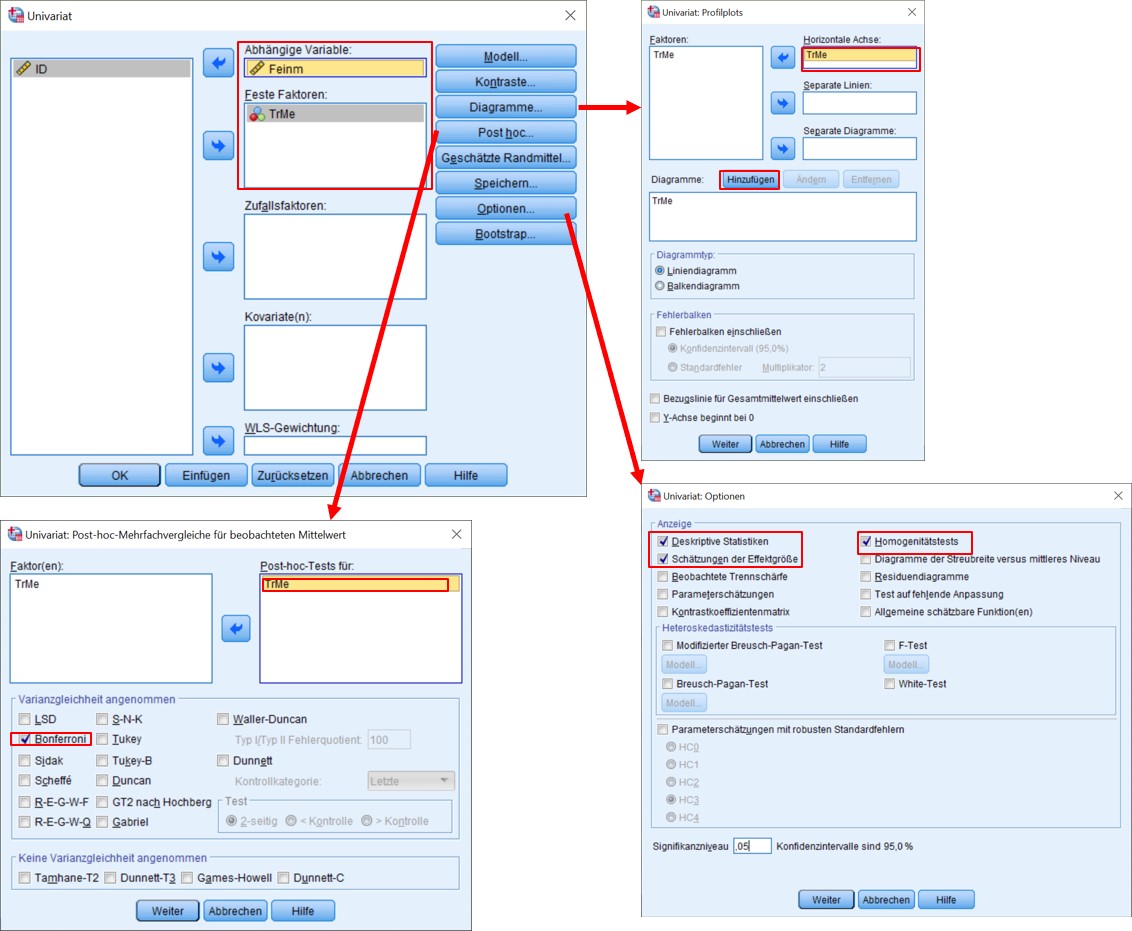
3.1. SPSS-Befehle
SPSS-Syntax
UNIANOVA Feinm BY TrMe
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=TrMe(BONFERRONI)
/PLOT=PROFILE(TrMe)
/INTERCEPT=INCLUDE
/CRITERIA=ALPHA(.05)
/DESIGN=TrMe.
3.2. Boxplots zur Illustration
Um einen ersten Überblick über die Daten zu gewinnen, empfiehlt es sich Boxplots zu erstellen. Diese können im SPSS-Menü erstellt werden: Grafik > Klassische Dialogfelder > Boxplot.
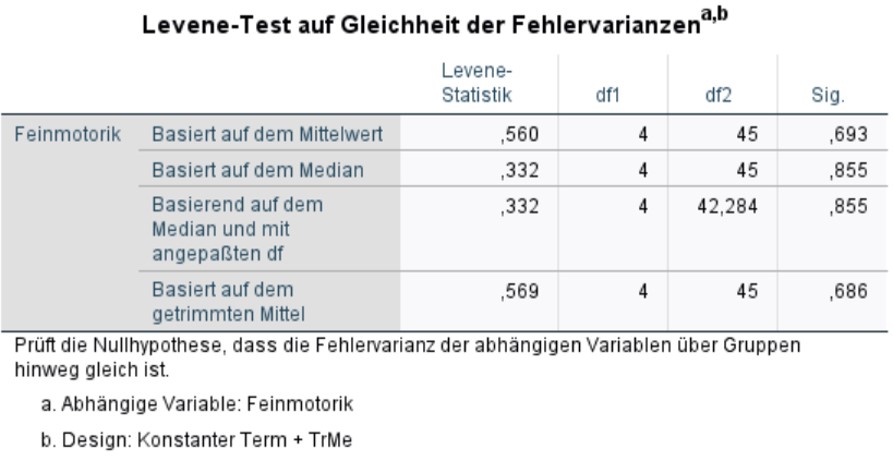
3.3. Prüfung der Varianzhomogenität (Levene-Test)
Der Levene-Test prüft die Nullhypothese, dass die Varianzen der Gruppen sich nicht unterscheiden. Ist der Levene-Test nicht signifikant, so kann von homogenen Varianzen ausgegangen. Wäre der Levene-Test jedoch signifikant, so wäre eine der Grundvoraussetzungen der Varianzanalyse verletzt. Gegen leichte Verletzungen gilt die Varianzanalyse als robust; vor allem bei genügend und etwa gleich grossen Gruppen sind Verletzungen nicht problematisch. Bei ungleich grossen Gruppen führt eine starke Verletzung der Varianzhomogenität zu einer Verzerrung des F-Tests. Alternativ können dann auf den Brown-Forsythe-Test oder den Welch-Test zurückgegriffen werden. Dabei handelt es sich um adjustierte F-Tests. In SPSS sind diese derzeit nur für einfaktorielle Varianzanalysen implementiert, wenn diese über das Menü Analysieren > Mittelwerte vergleichen > Einfaktorielle ANOVA durchgeführt werden (unter „Optionen“).
Im vorliegenden Beispiel ist der Levene-Test nicht signifikant (F(4,45) = .560, p = .693), so dass von Varianzhomogenität ausgegangen werden kann.
3.4. Ergebnisse der einfaktoriellen Varianzanalyse
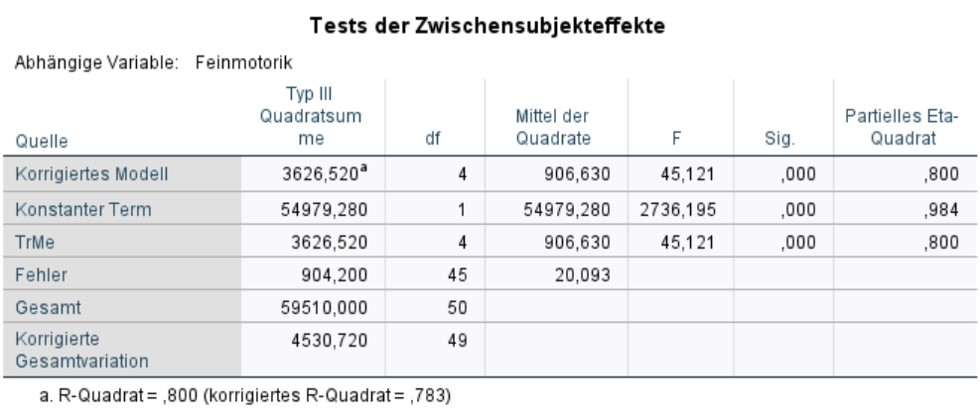
Signifikanz des Gesamtmodells und Modellgüte
Abbildung 7 zeigt den F-Test, der bereits im Kapitel Berechnung der Teststatistik vorgestellt wurde, in der Zeile „Korrigiertes Modell“. Der Test ist signifikant. Dies bedeutet, das Gesamtmodell ist signifikant (F(4,45) = 45.121, p < .001).
-
Als Fussnote beinhaltet Abbildung 7 zudem ein Mass für die Modellgüte: das korrigierte R-Quadrat. Dieses ist stets im Bereich von 0 bis 1 und gibt an, welcher Anteil der Streuung um den Gesamtmittelwert durch das Modell erklärt werden kann. Im vorliegenden Beispiel ist das korrigierte R-Quadrat = .783. Dies bedeutet, dass das Modell 78.3% der Streuung um den Gesamtmittelwert erklärt.
Signifikanz des Haupteffekts
Ein Haupteffekt ist der direkte Effekt eines Faktors auf die abhängige Variable. Im Falle der einfaktoriellen Varianzanalyse gibt es einen Haupteffekt: jener der Gruppierungsvariable. Bei einer mehrfaktoriellen Varianzanalyse dagegen gibt es einen Haupteffekt pro Faktor sowie weitere für deren Interaktionen.
Im Fall der einfaktoriellen Varianzanalyse ist der F-Test für das Gesamtmodell und der Test für den Haupteffekt identisch, wie sich auch an den Werten der Teststatistik F zeigt. (Das heisst, es muss nicht gesagt werden, dass Modell und Haupteffekt signifikant sind. Es genügt, die eine oder die andere Aussage zu machen.)
Für das vorliegende Beispiel zeigt die Zeile „TreMe“ in Abbildung 7, dass der Haupteffekt der Trainingsmethode (TrMe) auf die Feinmotorik (Feinm) signifikant ist (F(4,45) = 45.121, p < .001, ηp2 = .800).
Das partielle Eta-Quadrat
Das partielle Eta-Quadrat (partielles η2), das am rechten Rand der Tabelle in Abbildung 7 ausgegeben wird, ist ein Mass für die Effektgrösse: Es setzt die Variation, die durch einen Faktor erklärt wird, in Bezug mit jener Variation, die nicht durch Faktoren des Modells erklärt wird. Im Falle der einfaktoriellen Varianzanalyse ist das partielle Eta-Quadrat jener Anteil der korrigierten Gesamtvariation, der durch das Modell erklärt wird und entspricht damit dem R-Quadrat in der Fussnote von Abbildung 7:
Im vorliegenden Beispiel ist das partielle Eta-Quadrat =.800. Das heisst, es wird 80.0% der Variation in Feinm durch TrMe aufgeklärt.
3.5. Post-hoc-Tests
Multiples Testen
Obwohl der F-Test zeigt, dass ein Haupteffekt von TrMe auf Feinm besteht, muss anhand von Post-hoc-Tests geklärt werden, zwischen welchen Faktorstufen (Trainingsmethoden) signifikante Unterschiede bezüglich der Feinmotorik bestehen.
Bei der Berechnung von Post-hoc-Tests wird im Prinzip für jede Kombination von zwei Mittelwerten ein t-Test durchgeführt. Im aktuellen Beispiel mit fünf Gruppen sind dies 10 Tests. Multiple Tests sind jedoch problematisch, da der Alpha-Fehler (die fälschliche Ablehnung der Nullhypothese) mit der Anzahl der Vergleiche steigt. Wird nur ein t-Test mit einem Signifikanzlevel von .05 durchgeführt, so beträgt die Wahrscheinlichkeit des Nicht-Eintreffens des Alpha-Fehlers 95%. Werden jedoch zehn solcher Paarvergleiche vorgenommen, so beträgt die Nicht-Eintreffens-Wahrscheinlichkeit des Alpha-Fehlers (.95)10 = .598. Um die Wahrscheinlichkeit des Eintreffens des Alpha-Fehlers zu bestimmen, wird 1 – .598 = .402 gerechnet. Die Wahrscheinlichkeit des Eintreffens des Alpha-Fehlers liegt somit bei 40.2%. Diese Fehlerwahrscheinlichkeit wird als „Familywise Error Rate“ bezeichnet.
Um dieses Problem zu beheben kann zum Beispiel die Bonferroni-Korrektur angewandt werden. Hierbei wird α durch die Anzahl der Paarvergleiche dividiert. Im hier aufgeführten Fall ist dies .05/10 = .005. Das heisst, jeder Test wird gegen ein Niveau von .005 geprüft. Die Bonferroni-Korrektur führt zu eher konservativen Tests bezüglich des Alpha-Fehlers, während andere Korrekturen weniger konservativ sind. SPSS bietet eine grosse Auswahl an möglichen Korrekturen (vgl. Klicksequenz in Abbildung 3).
Post-hoc-Tests für das vorliegende Beispiel
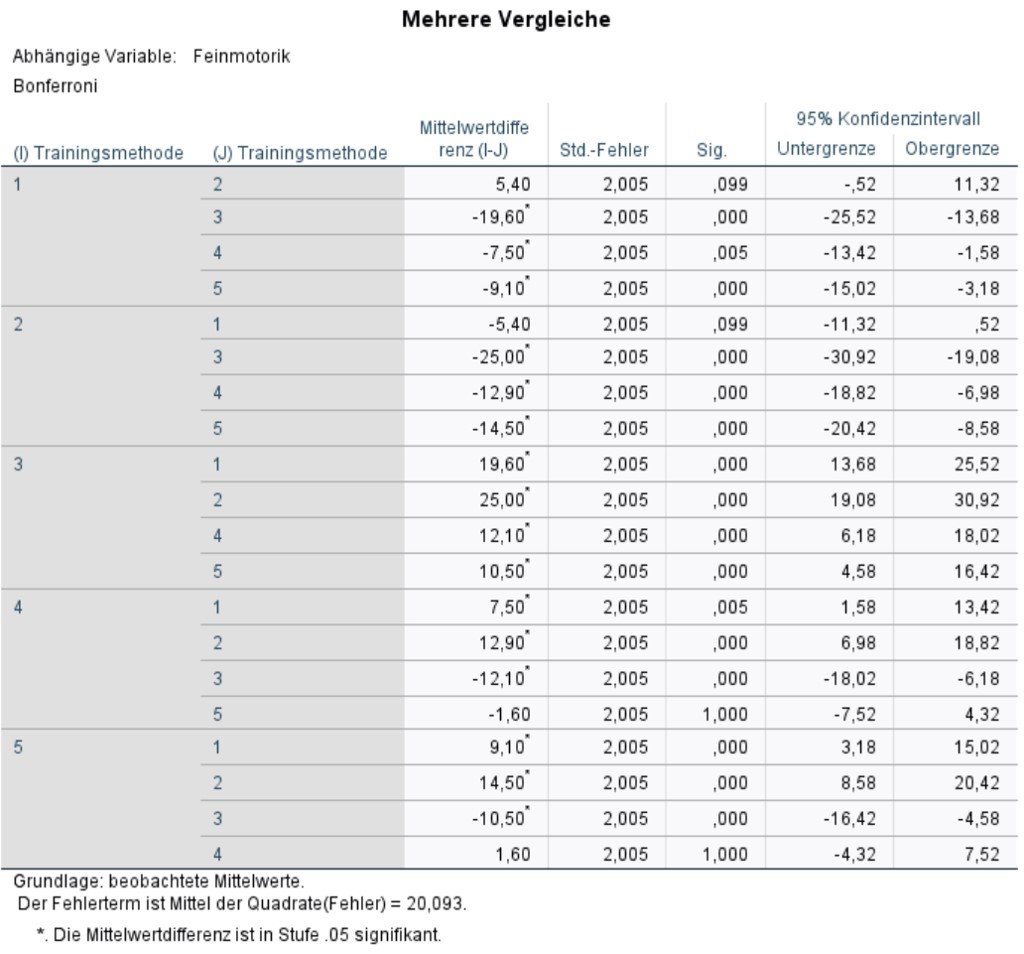
Abbildung 8 zeigt die Ergebnisse der Post-hoc-Tests mit Bonferroni-Korrektur. Es ist zu beachten, dass die p-Werte bereits von SPSS Bonferroni-korrigiert wurden und darum nun gegen .05 geprüft werden dürfen.
Es wird ersichtlich, dass sich die Trainingsmethoden 1 und 2 sowie 4 und 5 bezüglich der Feinmotorik nicht signifikant unterscheiden. Alle übrigen Trainingsmethoden unterscheiden sich signifikant (p < .05). Es können also drei Gruppen von Trainingsmethoden gebildet werden (Trainingsmethoden 1 und 2, Trainingsmethode 3, Trainingsmethoden 4 und 5).
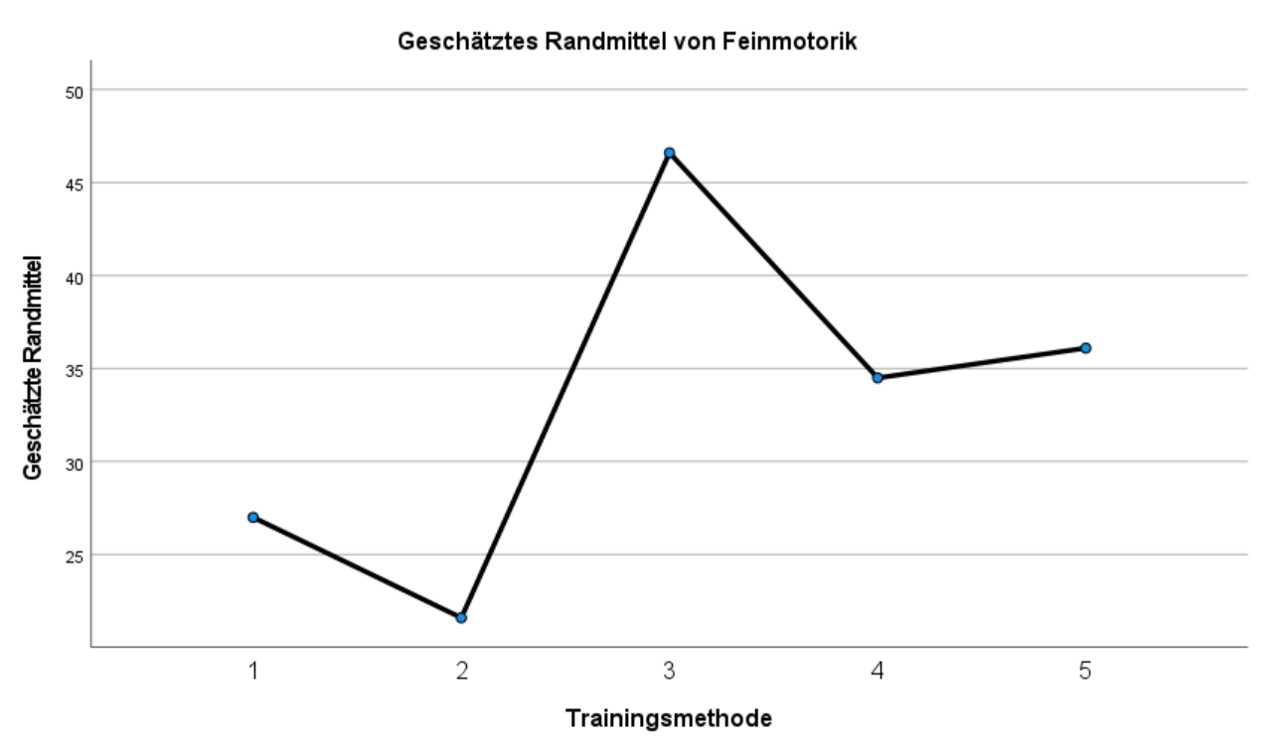
3.6. Profildiagramm
Das Profildiagramm in Abbildung 9 illustriert die Ergebnisse der Varianzanalyse. Während dieses Diagramm hier wenig zusätzliche Informationen beinhaltet, sind analoge Diagramme im Falle der mehrfaktoriellen Varianzanalyse äusserst hilfreich für die Interpretation der Ergebnisse.
3.7. Berechnung der Effektstärke
Um die Bedeutsamkeit eines Ergebnisses zu beurteilen, werden Effektstärken berechnet. Im Beispiel sind zwar einige der Mittelwertsunterschiede zwar signifikant, doch es stellt sich die Frage, ob sie gross genug sind, um als bedeutend eingestuft zu werden.
Es gibt verschiedene Arten, die Effektstärke zu messen. Zu den bekanntesten zählen die Effektstärke von Cohen (d) und der Korrelationskoeffizient (r) von Pearson. Für die einfaktorielle Varianzanalyse wird jedoch oft Cohen’s f verwendet, so auch im Folgenden.
Da SPSS das partielle Eta-Quadrat ausgibt, wird dieses hier in die Effektstärke f nach Cohen (1992) umgerechnet. In diesem Fall befindet sich die Effektstärke immer zwischen 0 und unendlich.
3.8. Eine typische Aussage
Die Auswahl der Trainingsmethode hat einen signifikanten Einfluss auf die Feinmotorik (F(4,45) = 45.121, p < .001, ηp2 = .800, n = 50). 78.3% der Streuung der Feinmotorik-Werte um den Gesamtmittelwert kann durch die Trainingsmethoden erklärt werden (korrigiertes R2). Die Effektstärke liegt bei f = 2.00 und entspricht einem starken Effekt nach Cohen (1988). Post-hoc-Tests mit Bonferroni-Korrektur zeigen, dass sich die Trainingsmethoden nicht alle signifikant unterscheiden. Methode 1 (M = 27.0, SD = 3.94) und 2 (M = 21.6, SD = 5.15) unterscheiden sich nicht signifikant voneinander. Methode 4 (M = 34.5, SD = 4.50) und 5 (M = 36.1, SD = 4.63) auch nicht. Einzig Methode 3 (M = 46.5, SD = 4.10) unterscheidet sich signifikant von allen anderen Methoden. Methode 3 scheint zudem auch am effektivsten zu sein.