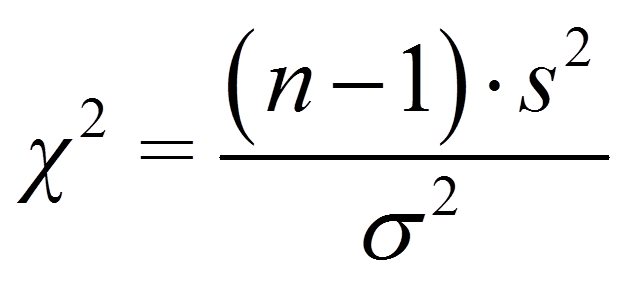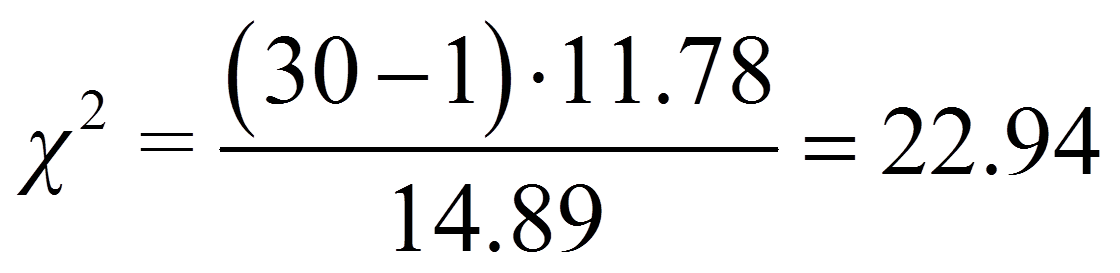 Quick Start
Quick Start
1. Einführung
1.1. Beispiele für mögliche Fragestellungen
1.2. Voraussetzungen der einfaktoriellen Varianzanalyse mit Messwiederholung
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
2.2. Berechnung der Teststatistik
3. Der Chi-Quadrat-Streuungstest mit SPSS
3.1. SPSS-Befehle
3.2. Ergebnisse des Chi-Quadrat-Tests
3.3. Eine typische Aussage
Quick Start
| Wozu wird der Chi-Quadrat-Streuungstest verwendet? Der Chi-Quadrat-Streuungstest testet, ob die Varianz einer Variable innerhalb einer Stichprobe (Stichprobenvarianz) mit deren Varianz in der Grundgesamtheit (Populationsvarianz) übereinstimmt. SPSS-Menü
Analysieren > Deskriptive Statistiken > Häufigkeiten SPSS-Syntax
FREQUENCIES VARIABLES= Variable /FORMAT=NOTABLE /STATISTICS=VARIANCE MEAN SPSS-Beispieldatensatz
Chi-Quadrat-Streuungstest |
1. Einführung
Der Chi-Quadrat-Streuungstest testet, ob die Varianz einer Variablen innerhalb einer Stichprobe (Stichprobenvarianz) mit deren Varianz in der Grundgesamtheit (Populationsvarianz) übereinstimmt. Daher wird auch von einem Test auf „Varianzhomogenität“ gesprochen. Es handelt sich dabei um ein nicht-parametrisches statistisches Verfahren mit einer Teststatistik, die einer Chi-Quadrat-Verteilung folgt.
Beim hier vorgestellten Chi-Quadrat-Streuungstest handelt es sich um einen ungerichteten Test. Das bedeutet, dass lediglich überprüft wird, ob Varianzunterschiede vorliegen. Die Richtung des Unterschiedes, also beispielsweise welche Varianz grösser ist, wird nicht beurteilt.
Die Fragestellung des Chi-Quadrat-Streuungstests wird oft so verkürzt: „Unterscheidet sich die Stichproben- und Populationsvarianz eines interessierenden Merkmals?“
1.1. Beispiele für mögliche Fragestellungen
- Gibt es einen Unterschied zwischen der Streuung des Gewinnes von Aktienkäufen durch Börsenmakler im Vergleich zur Streuung des Gewinns in der Gesamtheit der Aktienkäufer?
- Unterscheidet sich die Varianz der Qualität von Marken-T-Shirts im Vergleich zur Gesamtheit der hergestellten T-Shirts?
- Ist der Unterschied in der Varianz der Haltbarkeit von Freilandeiern und allen zum Verkauf produzierten Eiern zufällig?
- Unterscheidet sich die Streuung der Anzahl Gewürze, die Spitzenköche in einem Geruchstest erkennen, von der Streuung in der Gesamtheit der Berufsköche?
1.2. Voraussetzungen der einfaktoriellen Varianzanalyse mit Messwiederholung
| ✓ | Die Variable ist intervallskaliert |
| ✓ | Es liegen keine Ausreisser vor |
| ✓ | Das Merkmal ist in der Grundgesamtheit normalverteilt (Der Test ist nicht robust. Bereits relativ geringfügige Abweichungen beeinflussen das Ergebnis.) |
| ✓ | Die Varianz in der Grundgesamtheit muss bekannt sein |
2. Grundlegende Konzepte
2.1. Beispiel einer Studie
Eine Gruppe von Sportmedizinern untersucht die Verletzungshäufigkeit (Anzahl Sportverletzungen pro Jahr) von 30 Kampfsportlern im Vergleich zu Sportlern im Allgemeinen. Sie fragen sich, ob sich die Varianz der Verletzungshäufigkeit von Kampfsportlern von der Varianz in der Grundgesamtheit der Sportler unterscheidet.
Der zu analysierende Datensatz enthält neben der Probandennummer (ID) die Verletzungshäufigkeit der Sportler (Verletzungshäufigkeit).
Der Datensatz kann unter Quick Start heruntergeladen werden.
2.2. Berechnung der Teststatistik
Berechnung der Teststatistik
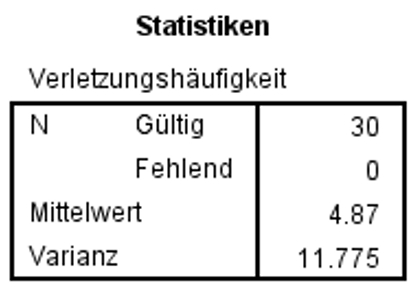
Zur Berechnung der Teststatistik wird die Populationsvarianz benötigt. Um diese zu ermitteln, ist es nicht notwendig, die komplette Population zu untersuchen, sondern es wird in der Regel auf die Varianz einer repräsentativen Stichprobe zurückgegriffen. Dies ist auch im vorliegenden Beispiel der Fall: Die Populationsvarianz, also die Varianz der Verletzungshäufigkeit in der Grundgesamtheit der Sportler, wurde in einer früheren Erhebung mittels einer repräsentativen Stichprobe erfasst und liegt damit bereits vor. Die Stichprobenvarianz dagegen wird auf Basis der Stichprobe von Kampfsportler ermittelt. Beide Varianzen sind in Abbildung 1 ersichtlich.
Um zu prüfen, ob sich die beiden Varianzen signifikant unterscheiden, wird die Teststatistik Chi-Quadrat (χ²) ermittelt. Sie wird wie folgt berechnet:
Signifikanz der Teststatistik
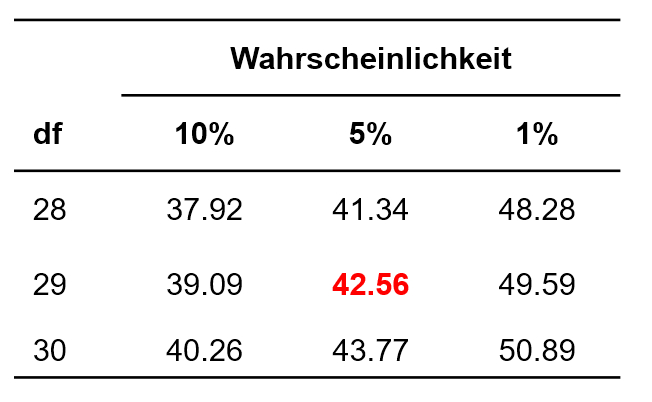
Der berechnete Wert muss nun auf Signifikanz geprüft werden. Dazu wird die Teststatistik mit dem kritischen Wert der durch die Freiheitsgrade (df) bestimmten Chi-Quadrat-Verteilung verglichen. Dieser kritische Wert kann Tabellen entnommen werden. Abbildung 2 zeigt einen Auszug.
Für das vorliegende Beispiel beträgt der kritische Wert 42.56 bei df = 29 und α = .05 (siehe Abbildung 2). Ist der Wert der Teststatistik höher als der kritische Wert, so ist der Unterschied signifikant. Dies ist für das Beispiel nicht der Fall (22.94 < 42.56). Es muss also davon ausgegangen werden, dass es keinen Unterschied zwischen der Varianz der Verletzungshäufigkeit von Kampfsportlern und jener der Grundgesamtheit der Sportler gibt (Chi-Quadrat(29) = 22.94, p > .05, n = 30).
3. Der Chi-Quadrat-Streuungstest mit SPSS
3.1. SPSS-Befehle
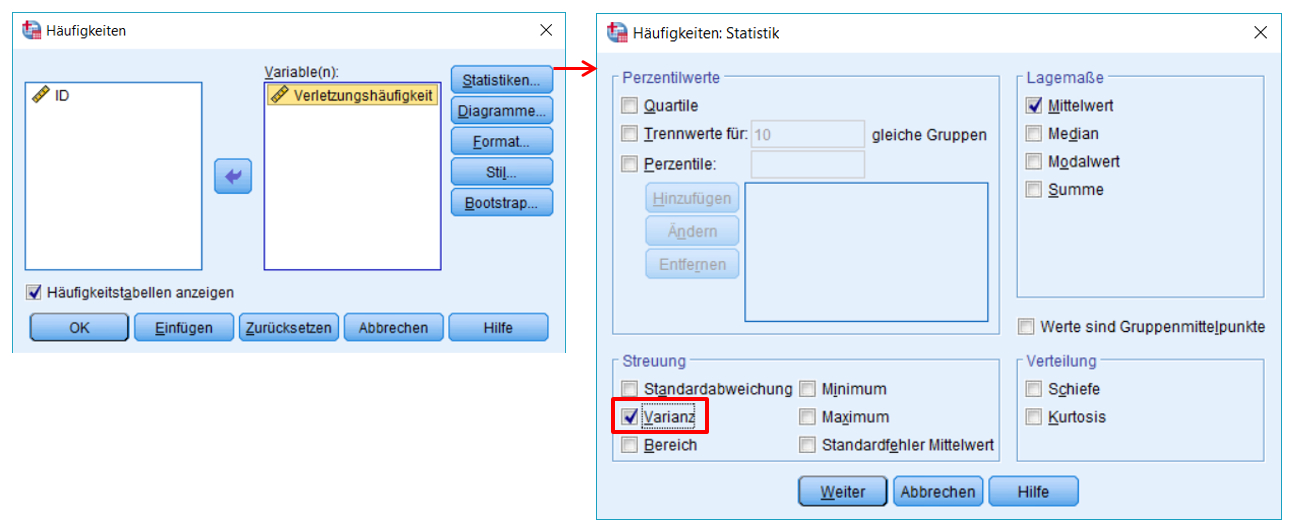
Es ist nicht möglich, den Chi-Quadrat-Streuungstest direkt mit SPSS durchzuführen. Die Varianz der Stichprobe kann jedoch mittels SPSS ermittelt werden, wie die Klicksequenz in Abbildung 3 zeigt.
SPSS-Menü: Analysieren > Deskriptive Statistiken > Häufigkeiten
Hinweis
- Unter Statistiken können die Kennwerte angegeben werden, die SPSS ausgeben soll. Zur manuellen Berechnung des Chi-Quadrat-Tests wird lediglich die Stichprobenvarianz benötigt.
SPSS-Syntax
FREQUENCIES VARIABLES=Verletzungshäufigkeit
/FORMAT=NOTABLE
/STATISTICS=VARIANCE MEAN
/ORDER=ANALYSIS.
Mit Hilfe der von SPSS ausgegebenen Stichprobenvarianz (Abbildung 4) lässt sich, wie im Unterkapitel Berechnung der Teststatistik beschrieben, der Chi-Quadrat-Wert ermitteln und das Signifikanzniveau bestimmen.
3.3. Eine typische Aussage
Die Varianz der Verletzungshäufigkeit von Kampfsportlern unterscheidet sich nicht signifikant von derjenigen von Sportlern im Allgemeinen (Chi-Quadrat-Streuungstest: Chi-Quadrat(29) = 22.94, p > .05, n = 30).